Philosophy, Computing, and Artificial Intelligence
PHI 319. Two Famous Experiments in Psychology.
Computational Logic and Human Thinking
Chapter 2 (38-53)
In this lecture, we consider two famous experiments in psychology.
These experiments seem to show something about how the human mind works. Because the goal in AI is not to implement the human mind on a machine, nothing directly follows about whether we can use logic programming to model the intelligence of a rational agent.
The Wason Selection Task
"Reasoning about a rule"," P. C. Wason. The Quarterly Journal of Experimental Psychology, 20:3,1968, 273-281. The "Wason Selection Task" refers to an experiment Peter Wason performed in 1968.
"The subjects [in a pilot study (Wason, 1966)] were presented with the following sentence, 'if there is a vowel on one side of the card, then there is an even number on the other side,' together with four cards each of which had a letter on one side and a number on the other side. On the front of the first card appeared a vowel (P), on the front of the second a consonant (P), on the front of the third an even number (Q), and on the front of the fourth an odd number (Q). The task was to select all those cards, but only those cards, which would have to be turned over in order to discover whether the experimenter was lying in making the conditional sentence. The results of this study, and that of a replication by Hughes (1966), showed the same relative frequencies of cards selected. Nearly all subjects select P, from 60 to 75 per cent. select Q, only a minority select not-Q and hardly any select not-P. Thus two errors are committed: the consequent is fallaciously affirmed and the contrapositive is withheld. This type of task will be called henceforth the 'selection task'" (Wason 1968: 273-274). The subjects in this experiment select from among presented options. This task is posed in terms of cards the subjects can see. There are four cards, with letters on one side and numbers on the other. The cards are lying on a table with only one side of each card showing:
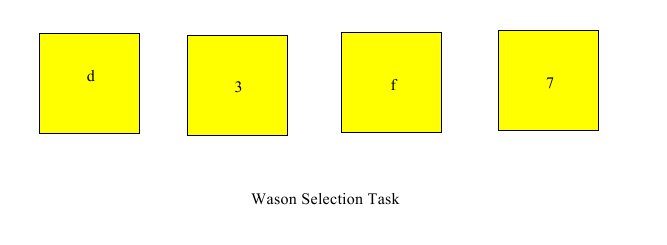
The task presented to the subjects is to select those and only those cards that must be turned over to determine whether the following statement is true:
If there is a d on one side, then there is a 3 on the other side.
Most people select differently on formally equivalent tasks but have more meaningful content.
Here is an example. Suppose that the task is to enforce the policy that
You must be at least twenty-one years old to drink in a bar
This task is equivalent to checking cases to determine the truth of the material conditional
If a person is drinking alcohol in a bar, then the person is at least twenty-one years old
Given the following mapping of the cards to the possibilities
card 1: person is drinking (alcholic) beer
card 2: person is a senior citizen
card 3: person is drinking (non-alcoholic) soda
card 4: person is a primary school child
most people know what to do. They know, for example, that given the "person is a primary school child," they must determine whether the "person is drinking alcohol in a bar." This corresponds to turning over the fourth card in the Wason Selection Task.
How to Explain the Observed Results
What is the explanation for these asymmetrical experimental results?
If the computations in logic programming are a good model of reasoning as it occurs in human beings, then one might think that subjects would be equally good at both selection tasks.
Why might one think this?
The ability to determine logical consequence is a fixed part of the logic programming/agent model. It is an innate part of the agent's mind, not something it must learn.
The conclusions in the following arguments are logical consequences of their premises:
P → Q P Q ¬P P → Q ¬Q
----------- ------- ------- --------------
Q P → Q P → Q ¬P
This means, in the case of the second and third cards, that once we observe "3" and "f" on the cards faces, we do not have to turn the cards over because the conditional follows as a logical of our observations. We observe "3" and "f." We put the corresponding beliefs in our KB. We ask ourselves whether the conditional is a logical consequence of our beliefs. The backward chaining computation returns the answer that it is a logical consequence.
We handle the first and fourth cards similarly. We observe "d" and "7." We put the corresponding beliefs in our KB. We ask ourselves if the conditional is a logical consequence of what we believe. The backward chaining computation answers that it is not a logical consequence. So we know we need to turn over the cards to get more information.
Determining the truth of the "alcohol" conditional is not meaningfully different.
We make the observations, put the corresponding beliefs in our KB, and use our innate ability to determine whether the conditional is a logical consequence of what we believe.
A Hypothesis about Logic from Evolutionary Psychology
"An evolutionary analysis suggests that these explanations fail because their basic assumption - that the same cognitive processes govern reasoning about different domains-is false. The more important the adaptive problem, the more intensely selection should have specialized and improved the performance of the mechanism for solving it (Darwin, I859/1958; Williams, 1966). Thus, the realization that the human mind evolved to accomplish adaptive ends indicates that natural selection would have produced special-purpose, domain- specific, mental algorithms-including rules of inference-for solving important and recurrent adaptive problems (such as learning a language; Chomsky, I975, 1980). It is advantageous to reason adaptively, instead of logically, when this allows one to draw conclusions that are likely to be true, but cannot be inferred by strict adherence to the propositional calculus. Adaptive algorithms would be selected to contain expectations about specific domains that have proven reliable over a species’ evolutionary history. These expectations would differ from domain to domain. Consequently, if natural selection had shaped how humans reason, reasoning about different domains would be governed by different, content-dependent, cognitive processes" (Leda Cosmides, "The logic of social exchange: Has natural selection shaped how humans reason? Studies with the Wason selection task," 193. Cognition, 31 (1989), 187-276). The evolutionary psychologist Leda Cosmides has challenged the assumption that human beings have an ability to determine logical consequence of the sort we are using.
To explain asymmetrical experimental results, she suggests that humans have evolved so that they possess a specialized algorithm to detect cheaters in social contracts.
Her idea is that the ability to reason about the connections between states in the world is not an instance of a single capacity human minds possess. Instead, human beings develop domain specific capacities at different ages. One of these is the capacity to detect cheaters.
(It might be too that in human beings domain specific capacities evolved from earlier, more primitive domain specific capacities. It might be, for example, that the ability to solve abstract mathematical problems evoled from the capacity for route planning. Many mathematicians appear to rely on something like "geometrical intuition" to guide their thinking about mathematical questions that bear no evident resemblance to navigational plotting.)
Since cooperation has survival value from an evolutionary perspective, and since cooperation is stable as long as cheaters are detected and deterred, it might be that one domain for reasoning is the "domain of social morality." If there were such a domain specific capacity for reasoning about cheaters, maybe this explains why people do better with the "alcohol" conditional than with the "cards with numbers and letters" conditional. Evolution has given humans the intelligence that makes them good at detecting cheaters but not at logical deduction in general.
Domain Specific Deduction and Logical Deduction
To think about Cosmides's hypothesis, it is necessary to think about logical consequence.
In reasoning, deduction is an activity in which an agent draws out implications of a set of premises. The agent reasons from premises to conclusions. Some but not all deductions are logical deductions. In logical deductions, the implications are logical consequences.
An example may help clarify the distinction between deductions and logical deductions.
In reasoning about an electrical circuit, one might reason from the premise that the switch is open to the conclusion that the lamp is off. This is a deduction, but it is not a logical deduction. The conclusion is a reasonable implication of the premise given how states are typically connected in electrical circuits, but the conclusion is not a logical consequence of the premise.
Domain Specific Deduction is more than Logical Deduction
What deductions are logical deductions?
Logical deductions are deductions the rules of logic permit. There is controversy among philosophers about what the rules of logic are, but we are not going to worry much about this.
For the sake of illustration, we are going to assume that what are sometimes called Disjunction-Introduction (∨I) and Disjunction-Elimination (∨E) as examples of the rules of logic.
These two deduction rules (∨I and ∨E) may be stated as follows:
P
------- ∨I
P ∨ Q
|
Q
------- ∨I
P ∨ Q
|
[P]¹ [Q]²
. .
. .
. .
P ∨ Q C C
------------------------- ∨E, 1, 2
C
|
∨I says that a disjunction is a logical consequence of either of its disjuncts. To see that the conclusion follows, we do not need to know anything more than the meaning of "or" (∨).
From the premise that "Tom teaches at ASU," it follows by ∨I that "Tom teaches at ASU, or the moon is made of cheese." Further, this consequence is not limited to specific domains. It is a consequence in every domain. It is a logical consequence of the premise.
∨E is a little less straightforward to understand.
∨E says that given deductions of a conclusion from the disjuncts of a disjunction, the conclusion is a consequence of the disjunction. If the deductions of the conclusion are logical deductions, then ∨E says that the conclusion is a logical consequence of the disjunction. If the deductions of the conclusion from the disjuncts are not logical deductions, ∨E says that the deduction of the conclusion from the disjunction is not a logical deduction.
The Capacity for Logical Deduction
Now it is possible to get a little clearer on the hypothesis from evolutionary psychology.
The idea is that the capacity to draw conclusions (make deductions) in certain domains is a capacity human beings naturally develop. The capacity for logical deduction, however, is not a capacity restricted to a domain. It is a capacity to make deductions in any domain. According to the hypothesis from evolutionary psychology, we do not naturally develop this capacity. Although it is something most of us can learn if we put in the time and effort, it is not something we acquire naturally as we become adults, like, say, our adult teeth.
Consider again the "electrical circuits" example.
We might ask ourselves whether from the premise that "the switch is open or closed," it follows that "the lamp is off or on." The proof would use a version of Disjunction-Elimination (∨E) in which the subproofs used the nonlogical premises that "if the switch is open, the lamp is off" and "if the switch is closed, the lamp is on." Experience has taught us to accept these premises, and we have the capacity to see that the conclusion is an implication.
In the case of the "alcohol" conditional, the query is passed to a part of the mind that deals with detecting cheaters (just as the query about electrical circuits is passed to a part of the mind that has experience with electrical circuits). This "cheater detection" part of the mind has developed in human beings because this ability gave human beings an evolutionary advantage.
Cosmides's hypothesis is that our minds are the product of evolution and that this process has not resulted in a part of the mind that deals with logical consequence. Our ability to answer questions about logical consequence develops as we take the time and make the effort to think about the difference between logical and nonlogical consequence. Since most of us have not done this (by, for example, taking and working hard in a philosophy class about logic), most of us do not have the ability to draw consequences from our observations of the cards in a way that tells us what to do to determine whether the "card" conditional is true.
An Alternative Explanation of the Observed Results
Robert Kowalski rejects the explanation of the results of the experiment in terms of the hypothesis from evolutionary psychology. He tries to understand the results in the two selections tasks in terms of the formula "Natural language understanding = translation into logical form + general purpose reasoning" (Computational Logic and Human Thinking, 217).
Kowalski's formula is not straightforward to understand, but his idea is that the subjects in the Wason Selection Task make the selections they do (not because they have not developed the capacity for logical deduction they use in what he calls "general purpose reasoning" but) because they understand the conditionals according to the framework of the logic programming/agent model. This understanding is not what the experimenters expect.
We will consider Kowalski's argument in more detail in a subsequent lecture.
We can see now, though, that Kowalski is trying to do something we are not. He is trying to defend the idea that the logic programming is a good model of human intelligence.
The Byrne Suppression Task
"Suppressing valid inferences with conditionals," R.M.J. Byrne. Cognition, 31, 1989, 61-83.
The "Byrne Suppression Task"
is an experiment Ruth Byrne conducted in 1989.
Like the Wason Selection Task, the Byrne Suppression Task seems to show something
about reasoning.
In the experiment, the subjects are asked to consider the following two statements:
If she has an essay to write, then she will study late in the library
She has an essay to write
On the basis of these two statements, most people in the experiment draw the conclusion that
She will study late in the library
However, given the additional information
If the library is open, then she will study late in the library
many people in the experiment, about 40%, "suppress" (or retract) their previous conclusion. According to classical logic, this "suppression" is a mistake. The conclusion (She will study late in the library) still follows as a logical consequence of the stated premises.
The argument has the following logical form:
1. If P, then Q If she has an essay to write, then she will study late in the library 2. P She has an essay to write 3. R If the library is open, then she will study late in the library ---- ---- 4. Q She will study late in the library
Like Disjunction-Introduction and Elimination, Conditional-Elimination is traditional rule of logic. The conclusion (Q) is a logical consequence of premises (1) and (2). The deduction from these premises proceeds by the rule of Conditional-Elimination (→ E):
P If P, then Q P P → Q
------------------ → E ------------ → E
Q Q
This is what is called is sometimes called monoticity. A "logic" (set of rules
for deduction) is monotonic just in case
if P1 ⊢ φ, then P1 U P2 ⊢ φ
Given this rule, the addition of the third premise (R) in the argument does nothing to change the fact that the conclusion is a logical consequence. It is just
extra information. If a conclusion is a logical consequence of a set of
premises, then it remains a logical consequence no matter how many additional
premises are added to the original set of premises.
How to Explain the Observed Results
What explains the results observed in the "Byrne Suppression Task" experiment?
Kowalski's Explanation
Robert Kowalski suggests, again, that the subjects do not understand the sentences in the way the experimenters expect and do not reason in the way the experimenters expect.
We will consider here the part of Kowalski's solution that seems to apply to the mind of any rational agent. The more specific part of his solution we will consider in a subsequent lecture.
Kowalski suggests that the subjects in the "Byrne Suppression Task" understand the premises and the conclusion in such a way that the premises are defeasible reasons to believe the conclusion. Further, they understand the new information to defeat this reasoning.
The logic programming/agent model (as we are currently understanding it as a way to answer queries in terms of backward chaining) does not implement defeasible reasoning.
This is a serious problem. It does not seem likely that the reasoning in any rational agent is restricted to logical deductions. Certainly this does not seem true for human beings.
Conclusive and Defeasible Reasoning
To understand this problem, we need to distinguish conclusive and defeasible reasoning.
In conclusive reasoning, the reasoning is the reasoning in making a logical deduction. Backward chaining provides an example. If a query is answered positively, there is a logical deduction of the query from premises in the KB. We can think that the agent is reasoning from its beliefs to the conclusion that the query is true. This reasoning is conclusive because additional beliefs in the KB do not undermine it. The conclusion remains a logical consequence.
Defeasible reasoning is much more difficult to characterize. This makes it difficult to implement this kind of reasoning on machine. To implement it, we need to understand it.
It is easiest to understand defeasible reasoning when the agent is reasoning from premises to a conclusion. In this case, the reasoning is defeasible if new beliefs can make it rational to retract the belief in the conclusion while at the same time retaining the belief in the premises.
An example of defeasible reasoning helps make this sort of reasoning a little clearer.
An Undercutting Defeater
Suppose someone has the following beliefs:
• Ornithologists are reliable sources of information about birds
• Herbert is an ornithologist
• Herbert says that not all swans are white
Based on these premises, it is reasonable to draw the conclusion and to believe that
• Not all swans are white
The conclusion is not a logical consequence of the premises. There is no logical deduction from the premises to the conclusion, but the conclusion is a reasonable consequence.
If, however, one were later to come to know that Herbert is incompetent, this new information would undercut the reasoning to the conclusion that not all swans are white. What the agent comes to know about Herbert defeats the reason the premises give him to believe that not all swans are white. In these circumstances, it is rational for the agent to keep his belief in the premises but to retract his belief in the conclusion of the argument.
This seems to be an instance of how human beings form and retract beliefs. The problem is how to characterize it in sufficient detail so that it can be implemented on a machine.
Justification for Belief
There is another example that looks like but may not be an instance of defeasible reasoning.
Suppose that I form the belief that some object is red because it looks red. The proposition
The object is red
is not a logical consequence of the proposition
The object looks red to me.
Still, in ordinary circumstances, the object looking red makes it rational to believe it is red.
Suppose I form the belief that the object is red because it looks red. Suppose, however, that later I acquire new information. Suppose I come to know that the object is illuminated by a red light and that red lights can make white objects look red. This new information does not change the way the object looks to me. It still looks red to me. It might even be red, but no longer is it rational for me to believe that it is red because it looks red to me.
In this example, it is not clear that any reasoning is undercut
because it is not clear that
What happens, it seems, in the "looks red/is red" example is that instead of forming the belief by reasoning, I have a certain
experience (the experience of the object looking red to me) that justifies me in
believing the propositional content of this experience (that the object is red).
Another way to think about this is in terms of impressions. An impression is the way
things appear to the agent. I can have the impression that the object is red because this is
how it looks to me (as opposed, say, to having the impression because someone told me
that the object is red or because I measured
the wavelength of the light reflected from the object).
If there is no contrary information, then when someone gets the impression that
some object is red because it looks red, this experience justifies him in believing (or makes
it rational for him to believe) that the object is red.
This justification the experience provides does not guarantee that the propositional content of the impression is true.
The object might look but not be red. Further,
as the "looks red/is red" example shows, this justification can be defeated. If it is,
then because the proposition that object is red is no longer part of the agent's evidence,
he should abandon his belief in this proposition
because he can no longer
use it in reasoning.
I form the belief that the object is red by reasoning from
the belief that the object looks red. Rather, it seems that my experience makes it
rational for me to believe the object is red.
It is still true that new information can defeat my justification for the belief, but this defeat does not seem to be a matter of undercutting some reasoning I used to form the belief.
This, if we are thinking about the phenomenon correctly, tell us something interesting about justification. Sometimes the justification for a belief consists in reasoning. This is what happens in the "ornithologist" example. Sometimes, though, the justification consists in an experience rather than in reasoning. This is what happens in the "looks red/is red" example.
An Rebutting Defeater
In addition to undercutting defeaters, there are rebutting defeaters.
Suppose I form the belief that all A's are B's because I have seen many A's and they have all been B's. This conclusion that all A's are B's is not a logical consequence. Still, in the absence of contrary information, the premise makes it reasonable for me to believe that all A's are B's.
Now, though, suppose that I see an A that is not a B.
It is still rational for me to believe that the A's I saw in the past were all B's, but no longer is it rational for me to believe that all A's are B's. When I see A that is not a B, this new information rebuts my belief that all A's are B's and thus makes it rational for me to abandon this belief.
Again, this seems to be an instance of how humans form and retract beliefs.
What we have Accomplished in this Lecture
We looked at two famous experiments in psychology (the Wason Selection Task and the Byrne Suppression Task) that challenge assumptions about how the human mind works and about its ability to compute logical consequence. Further, we looked at the beginnings of Robert Kowalski's responses to these two experiments. In doing this, we looked at Leda Cosmides's hypothesis in evolutionary psychology that understands the ability to deduce logical consequences not as an innate part of the human mind but as a skill that must be learned. We also looked at conclusive and defeasible reasoning. We noted that the logic programming/agent model, as we have developed it so far, is limited to conclusive reasoning.

