Classical First-Order Logic
Three Natural Deduction Systems
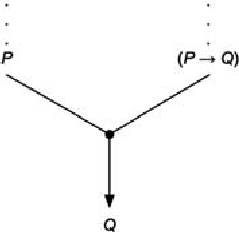
This inference graph represents what is called "conditional elimination" (→E).
Reasoning to φ and reasoning to φ → ψ can be joined to constitute
reasoning to ψ.
The inference graph for →E may be represented slightly more simply
if the node connecting the premises to the conclusion is replaced by a straight line.
Some of our reasoning in constructing proofs proceeds by joining stretches of reasoning together to reach a conclusion.
In many formal logic classes,
this process is represented in a slightly unnatural way. It is represented
as linear sequences of propositions, with each member of the sequence
being either a premise or the conclusion of an inference (in accordance with some
deduction rule) from earlier propositions in the sequence. This representation is unnatural because the
ordering of the elements of the sequence is not always essential to the reasoning itself.
It is more natural to represent the reasoning in terms of an inference graph. When deductions are represented in this way, the deductions are said to be written in the "Gentzen-style."
Introduction and Elimination Rules
In Gentzen-style deductions, each connective (¬, ∧, ∨, →, ∀, ∃) in the language has what are called "introduction" and "elimination" rules.
"The introductions represent, as it were, the 'definitions' of the symbols concerned, and the eliminations are no more, in the final analysis, than the consequences of these definitions" (The Collected Papers of Gerhard Gentzen, edited by M. E. Szabo (North Holland, 1969), 80).
Negation Introduction and Elimination
Negation(¬) has an introduction rule and an elimination rule. The rules are pretty straightforward. The introduction rule says that we are permitted to introduce ¬φ if we have ⊥. If ⊥ depends on an assumption φ, we are permitted to discharge this assumption when we introduce ¬φ.
[φ]¹
.
.
.
⊥ φ ¬φ
------- ¬I,1 ------- ¬E
¬φ ⊥
Conjunction Introduction and Elimination
Conjunction has an introduction and two elimination rules (as either conjunct can be eliminated).
φ ψ φ ∧ ψ φ ∧ ψ
------- ∧I ------- ∧E ------- ∧E
φ ∧ ψ φ ψ
Disjunction Introduction and Elimination
Disjunction has two introduction rules (as either disjunction is sufficient) and an elimination rule.
[φ]¹ [ψ]²
. .
. .
. .
φ ψ φ ∨ ψ χ χ
------- ∨I ------- ∨I ------------------------ ∨E, 1, 2
φ ∨ ψ φ ∨ ψ χ
Conditional Introduction and Elimination
The conditional (or implication) has an introduction rule and an elimination rule.
[φ]¹
.
.
.
ψ φ φ → ψ
------- →I,1 ---------- →E
φ → ψ ψ
Minimal, Intuitionistic, and Classical Logic
A natural deduction system is characterized by the use of introduction and elimination rules together with the introduction of assumptions (which is permitted at any point in a proof).
The introduction and elimination rules in minimal logic are ¬I, ¬E, ∧I, ∧E, ∨I, E, →I, and →E.
The introduction and elimination rules for intuitionistic logic are the rules for minimal logic and the intuitionistic absurdity rule (ex falso quodlibet):
⊥ ---- ⊥I φ
The introduction and elimination rules for classical logic are the rules for intuitionistic logic together with the classical absurdity rule:
[¬φ]¹
.
.
.
⊥
---- ⊥C,1
φ
Constructing Proofs
"φ ⊢ ¬¬φ" asserts that there is a proof of ¬¬φ from the premise
φ. To say there is a proof of a conclusion from a set of premises is to say that it is possible in a finite number of steps to derive
the conclusion from the premises using the introduction and elimination rules in a way in which the conclusion
depends on no undischarged assumptions.
Here is proof written in the "Fitch-style":
|1. φ premise
|---
| | 2. ¬φ assumption
| |--
| | 3. φ reiteration. 1
| | 4. ⊥ ⊥-I, 2, 3
| 5. ¬¬φ ¬-I, 2-4
Frederick Fitch, (1908-1987). Symbolic Logic, An Introduction, The Ronald Press Company, 1952.
φ ⊢ ¬¬φ
[¬φ]¹ φ
--------- ¬E
⊥
------ ¬I,1
¬¬φ
To construct a proof, it often helps to begin by placing the conclusion at the bottom
------
¬¬φ
Now we work up toward the premises. We can get to ¬¬φ by using ¬-introdution. This gives us ¬φ as an assumption and ⊥ as the penultimate step
[¬φ]¹
---------
⊥
------ ¬I
¬¬φ
To get ⊥, we can use ¬-elimination. This requires φ, which is given as a premise for the proof
[¬φ]¹ φ
--------- ¬E
⊥
------ ¬I,1
¬¬φ
An example with →I shows that rules with assumptions permit them but do not require them.
⊢ ψ → (φ → ψ)
[ψ]1
------ →I
φ → ψ
--------- →I, 1
ψ → (φ → ψ)
Some Proofs in the Propositional Calculus
The realist accepts double negation elimination. Reality is determinate, and so it is one way or the other. The intuitionist rejects the proof. For the intuitionist, reality is not determinate. It may be that neither ¬φ nor φ is true. ¬¬φ ⊢ φ
[¬φ]¹ ¬¬φ
------------ ¬E
⊥
------ ⊥C,1
φ
φ ∨ ¬φ, ¬¬φ ⊢ φ
[¬φ]² ¬¬φ
------------ ¬E
⊥
------ ⊥I
φ ∨ ¬φ [φ]¹ φ
------------------------- ∨E, 1, 2
φ
"The long belief in the universal validity of the principle of excluded third in mathematics is considered by intuitionism as a phenomenon of history of civilization of the same kind as the old-time belief in the rationality of π or in the rotaton of the firmament on an axis passing through the earth. And intuitionism tries to explain the long persistence of this dogma by two facts: firstly, the obvious noncontradictory of the principle for an arbitrary single assertion; secondly the practical validity of the whole of classical logic for an extensive group of simple everyday phenomena. The latter fact apparently made such a strong impression that the play of thought that classical logic originally was, became a deep-rooted habit of thought which was considered not only as useful but even as aprioristic" (L.E.J. Brouwer, "Consciousness, Philosophy and Mathematics" (Proceedings of the 10th International Congress of Philosophy, Amsterdam 1948, 3: 1235–1249). ⊢ φ ∨ ¬φ
[φ]²
----- ∨I
φ ∨ ¬φ [¬(φ ∨ ¬φ)]¹
------------------------- ¬E
⊥
----- ¬I,2
¬φ
------ ∨I
φ ∨ ¬φ [¬(φ ∨ ¬φ)]¹
-------------------------- ¬E
⊥
------ ⊥C,1
φ ∨ ¬φ
"Peirce's Law." Charles Pierce, (1839–1914). ⊢ ((φ → ψ) → φ) → φ
[¬φ]² [φ]³
----------- ¬E
⊥
------ ⊥I
ψ
------- →I, 3
[(φ → ψ) → φ]¹ φ → ψ
-------------------------- →E
φ [¬φ]²
------------------- ¬E
⊥
--------⊥C, 2
φ
------------------ →I
((φ → ψ) → φ) → φ
→ is not definable in terms of ¬ and ∨ in intuitionistic logic. ¬φ ∨ ψ ⊢ φ → ψ
[¬φ]¹ [φ]³
---------- ¬E
⊥
------ ⊥I
¬φ ∨ ψ ψ [ψ]²
----------------------------- ∨E, 1, 2
ψ
-------- →I,3
φ → ψ
φ → ψ ⊢ ¬φ ∨ ψ
[φ]² φ → ψ
-------------- →E
ψ
-------- ∨I
¬φ ∨ ψ [¬(¬φ ∨ ψ)]¹
--------------------------- ¬E
⊥
------ ¬I,2
¬φ
------- ∨I
¬φ ∨ ψ [¬(¬φ ∨ ψ)]¹
----------------------------- ¬E
⊥
-------- ⊥C,1
¬φ ∨ ψ
Not all the contrapositive relationships are provable in intuitionistic logic. φ → ψ ⊢ ¬ψ → ¬φ
[φ]² φ → ψ
------------- →E
[¬ψ]¹ ψ
------------- ¬E
⊥
------ →I,2
¬φ
--------- →I,1
¬ψ → ¬φ
¬ψ → ¬φ ⊢ φ → ψ
[¬ψ]² ¬ψ → ¬φ
------------------- →E
[φ]¹ ¬φ
------------- ¬E
⊥
------ ⊥C,2
ψ
------- →I,1
φ → ψ
φ → ¬ψ ⊢ ψ → ¬φ
[φ]² φ → ¬ψ
------------------ →E
[ψ]¹ ¬ψ
------------- ¬E
⊥
------ ¬I,2
¬φ
------ →I,1
ψ → ¬φ
¬φ → ψ ⊢ ¬ψ → φ
[¬φ]² ¬φ → ψ
----------------- →E
[¬ψ]¹ ψ
--------------- ¬E
⊥
------ ⊥C,2
φ
------ →I,1
¬ψ → φ
¬φ ∨ ¬ψ ⊢ ¬(φ ∧ ψ)
[φ ∧ ψ]3 [φ ∧ ψ]3
--------- ---------
φ ¬φ1 ψ ¬ψ2
--------- ---------
¬φ ∨ ¬ψ ⊥ ⊥
----------------------------------------- ∨E, 1,,2
⊥
------- ¬I,3
¬(φ ∧ ψ)
¬(φ ∧ ψ) ⊢ ¬φ ∨ ¬ψ
[¬φ]2 [¬ψ]3
--------- ---------
¬φ ∨ ¬ψ [¬(¬φ ∨ ¬ψ)]1 ¬φ ∨ ¬ψ [¬(¬φ ∨ ¬ψ)]1
---------------------------- -----------------------------
⊥ ⊥
---- ⊥C,2 ---- ⊥C,3
φ ψ
--------------------------------
¬(φ ∧ ψ) φ ∧ ψ
---------------------------------------
⊥
-------- ⊥C,1
¬φ ∨ ¬ψ
¬(φ ∨ ψ) ⊢ ¬φ ∧ ¬ψ
[φ]1 [ψ]2
---- ----
¬(φ ∨ ψ) φ ∨ ψ φ ∨ ψ ¬(φ ∨ ψ)
-------------------- -------------------
⊥ ⊥
---- ¬I,1 ---- ¬I,2
¬φ ¬ψ
-------------------------
¬φ ∧ ¬ψ
¬φ ∧ ¬ψ ⊢ ¬(φ ∨ ψ)
¬φ ∧ ¬ψ ¬φ ∧ ¬ψ
---------- ---------
[φ]2 ¬φ [ψ]3 ¬ψ
-------------- ¬E ----------- ¬E
[φ ∨ ψ]1 ⊥ ⊥
------------------------------------------- ∨ E, 2, 3
⊥
------ ¬I,1
¬(φ ∨ ψ)
Some Proofs in the First-Order Predicate Calculus
The introduction and elimination rules in the first-order predicate calculus are the introduction and elimination rules in the propositional calculus and the introduction and elimination rules for the two quantifiers (the "universal" ∀ and "existential" ∃ quantifiers).
[φ(a)]¹
.
.
.
φ(a) ∀xφ(x) φ(t) ∃xφ(x) ψ
------- ∀I ------- ∀E ------ ∃I ---------------- ∃E,1
∀xφ(x) φ(t) ∃xφ(x) ψ
If a in does not occur in any premises on which φ(a) depends, then substitution converts the proof
into a proof of φ(t), for any term t. In this way, the idea underlying
∀I is that a proof of φ(a) for an arbitrary a is a proof ∀xφ(x).
From ∃xFxa, were a is arbitrary, we cannot conclude ∀x∃xFxx (but we can instead conclude ∀y∃xFxy).
• In ∀I,
x replaces every occurrence of a in φ(a),
a is not in the scope of a quantifier binding x in φ(a),
a does not occur in any premise on which φ(a) depends (and so is "arbitrary").
• In ∀E, t replaces every free occurrence of x in φ(x).
• In ∃I, the occurrences of t replaced by x cannot occur in the scope of a quantifier binding x.
• In ∃E,
a is not in ∃xφ(x),
a is not in ψ,
a is not in any assumption
(other than φ(a)) on which the upper occurrence of ψ depends.
∀ and ∃ are not interdefinable in terms of ¬ in intuitionistic logic. ¬∀xFx ⊢ ∃x¬Fx
[¬Fa]²
------- ∃I
[¬∃x¬Fx]¹ ∃x¬Fx
---------------------- ¬E
⊥
-------- ⊥C,2
Fa
------- ∀I
¬∀xFx ∀xFx
-------------- ¬E
⊥
-------- ⊥C,1
∃x¬Fx
∃x¬Fx ⊢ ¬∀xFx
[∀xFx]¹
-------- ∀E
[¬Fa]² Fa
--------------- ¬E
∃x¬Fx ⊥
--------------- ∃E,2
⊥
----- →I,1
¬∀xFx
¬∃xFx ⊢ ∀x¬Fx
[Fa]¹
---- ∃I
∃xFx ¬∃xFx
------------ ¬E
⊥
---- ¬I,1
¬Fa
------ ∀I
∀x¬Fx
∀x¬Fx ⊢ ¬∃xFx
∀x¬Fx
------- ∀E
[Fa]² ¬Fa
-------------- ¬E
[∃xFx]¹ ⊥
-------------------- ∃E,2
⊥
----- ¬I,1
¬∃xFx
∀xFx ⊢ ¬∃x¬Fx
∀xFx
----- ∀E
[¬Fa]² Fa
--------------- ¬E
[∃x¬Fx]¹ ⊥
-------------------------- ∃E,2
⊥
----- ¬I,1
¬∃x¬Fx
¬∃x¬Fx ⊢ ∀xFx
[¬Fa]¹
-------- ∃I
¬∃x¬Fx ∃x¬Fx
-------------------- ¬E
⊥
------ ⊥C,1
Fa
------- ∀I
∀xFx
¬∀x¬Fx ⊢ ∃xFx
[Fa]¹
-------- ∃I
[¬∃xFx]² ∃xFx
-------------------- ¬ E
⊥
--------- ¬I,1
¬Fa
---------- ∀I
∀x¬Fx ¬∀x¬Fx
------------------------- ¬E
⊥
--------- ⊥C,2
∃xFx
¬∀x¬Fx ⊢ ∃xFx
[Fa]¹
-------- ∃I
[¬∃xFx]² ∃xFx
---------------------- ¬ E
⊥
-------- ¬I,1
¬Fa
---------- ∀I
∀x¬Fx ¬∀x¬Fx
-------------------------- ¬E
⊥
--------- ⊥C,2
∃xFx
∃xFx ⊢ ¬∀x¬Fx
[∀x¬Fx]²
--------- ∀E
[Fa]¹ ¬Fa
--------------- ¬ E
∃xFx ⊥
--------------------------- ∃E,1
⊥
---------- ¬I 2
¬∀x¬Fx
