Philosophy, Computing, and Artificial Intelligence
PHI 319. Thinking is Computation.

"A Proposal for the Dartmouth Summer Research Project on Artificial Intelligence," 1955.
The Dartmouth College Artificial Intelligence Conference: The Next Fifty Years,
AI Magazine, Volume 27 Number 4, 2006.
Other Historical Documents:
"The Logic Theory Machine," 1963.
To say that "human beings are rational agents" is to attribute to them a certain ability and
to say they are subject to criticism if they do not exercise this ability correctly. It
is not to say that their beliefs and actions
are always rational. We know that is not true.
Robert Kowalski. Computational Logic and Human Thinking.
Introduction (14-21) Chapter 1 (22-37).
Hector Levesque. Thinking as Computation.
Chapter 1 (1-5, 11-21), Chapter 2 (23-38).
Artificial Intelligence
AI is about something. In this course, it is about intelligence.
The study of intelligence is not the same as cognitive science. Cognitive science is a study of human intelligence, how the human mind represents and manipulates knowledge and how mental representations and processes are realized in the brain.
The intelligence that interests us is the intelligence that characterizes a rational agent.
What is a rational agent? What is the intelligence of a rational agent?
Rational agents have goals, beliefs, and take actions based on their beliefs to satisfy their goals. Human beings are rational agents, and their intelligence is a primary example of the intelligence of a rational agent we seek to understand and model.
Human beings also have the ability to think some about whether their thought processes and actions are rational, and we are going to rely on this ability in our study of the intelligence of a rational agent. We are going to exercise of this ability to think about whether our thoughts and actions in the effort to design the "mind" of a (not very intelligent) rational agent.
Can we say more about what rationality and intelligence are?
The Rationality of an Agent
If to give a definition is to give a set of illuminating necessary and sufficient conditions, it may not be possible to give a definition of rational. We can, though, increase our understanding by considering two definitions of rational action that may initially seem plausible but in fact are open to counterexample and hence are false. (This will also provide an introduction to some of the practices and investigative techniques in philosophy.) The background assumption for these two definitions is that an agent is rational just in case its actions are rational.
The claims about what rational action is take the
form of "___ if and only if ___" claims of necessity.
For such claims to be true, the statements in the blanks on the two sides of the
biconditional (the "if and only if") cannot vary in truth-value. So one way to try to show that the biconditional is not true
is to imagine a situation in which
one of the statements is true and the other is false. The more plausible it is to think the imagined situation is possible,
the more plausible it is to think that the situation imagined is a
counterexample to the "___ if and only if ___" claim whose truth we are evaluating.
The following are different ways to say the same thing:
• If P is true, then Q is true
• The truth of P is sufficient for the truth of Q
• The truth of Q is necessary for the truth of P.
We might think that
(*) an action is rational if and only if (henceforth abbreviated as "iff") the action
accomplishes the agent's intended goal in performing the action.
This definition characterizes rational action in terms of the success of the outcome.
A little reflection, however, shows that this account of rational action is open to counterexample and hence is false. In the case of human beings, it is commonplace to think that some actions are rational even though they do not accomplish the agent's goal and that some actions are not rational even though they do accomplish the agent's goal.
Suppose that someone gets a flu shot because he wants to avoid the flu. If he later comes down with the flu, this itself is no reason to think that getting the shot was not rational. Success, then, as this example shows, is not a necessary condition for rational action. An action might be rational even though it does not accomplish the goal the agent intended to achieve.
Neither is success a sufficient condition for rational action.
Suppose that someone uses his life savings to buy tickets in a lottery. He knows that the probability of a given ticket winning is extremely small, but this does not bother him because he has a feeling that today is his lucky day. In this situation, buying the ticket is not rational even if he wins the lottery. So once again there is a counterexample to (*).
What conclusion about rational action can we draw from these counterexamples?
The following are different ways to say the same thing:
• If P is true, then Q is true
• P is true only if Q is true
• Q is true if P is true
Cognition is subject to evaluation as rational or irrational if it is something the
agent can control. So, for
example, when some object looks red to me, the looking red is something that happens to
me because of how my eyes and brain work. It is not subject to evaluation as rational or irrational. If,
however, I form the belief that the object is red, this belief is subject to evaluation.
I do not have to form the belief.
In thinking about these counterexamples, it appears that
rationality consists in thinking correctly and that actions are rational if they are the product of such thinking.
What it is to think (or cognize) correctly?
Even if we cannot answer this question, it seems clear that we can sometimes recognize instances of rational and irrational thinking in ourselves and in others. Otherwise, we would not have been able to assess the imagined examples as counterexamples to the proposed definitions of rational action. In this course, this ability to recognize instances is enough for us to begin to construct a model of the intelligence of a rational agent.
Russell and Norvig's Definition
Stuart Russell and Peter Norvig (authors of a once and maybe still popular textbook on AI) define rationality in terms of what they call a "performance measure" and its "maximization."
"For each possible percept sequence, a rational agent should select an action that is expected to maximize its performance measure, given the evidence provided by the percept sequence and whatever built-in knowledge the agent has" (Artificial Intelligence. A Modern Approach, 37).
As an example to illuminate the usefulness of their definition, they consider a vacuum cleaner agent. Its environment consists in two locations (A and B) arranged next to each other (A B). These locations can be clean of dirty. The agent (the vacuum cleaner) is capable of performing the following actions: it can perceive its current location, perceive whether this location is dirty or clean, can suck in its current location, can move to A, and can move to B.
About their example, we can ask the following question. To be a rational agent, as opposed to a mere machine, how should the vacuum cleaner "think" so that its actions are rational?
Here is one possible answer set in the context of an observation-thought-decision-action cycle:
1. Perceive current location and whether it is dirty or clean
2. If the location is dirty, suck
3. If the location is A, move to B
4. If the location is B, move to A
5. Repeat (go to 1)
Does the vacuum cleaner possess concepts?
It can discriminate between dirty and clean.
Is this enough for it to have concepts of dirty and clean?
What is it for something to have a concept?
"We might train a parrot reliably to respond differentially to the visible presence of red things by
squawking 'That’s red.' It would not yet be describing things as red,
would not be applying the concept
red to them, because the noise it makes has no significance for it. It does not know that it follows from
something’s being red that it is colored, that it cannot be wholly green, and so on. Ignorant as it is of those
inferential consequences, the parrot does not grasp the concept..."
(Robert Brandom, "How Analytic Philosophy Has Failed Cognitive Science").
Is this "thinking" and "acting" rational or irrational? Or is it not thinking and acting at all?
In trying to answer this question, it is not a problem to say whether the vacuum cleaner agent does what we want it to do. If we want it to keep A and B clean, this "thinking" and "acting" makes it do what we want. So, as a result, we might appraise the vacuum cleaner positively. We might say that it is a good vacuum cleaner and that it performs its function well.
Compare this vacuum cleaner to one whose observation-thought-decision-action cycle is
1. Perceive current location and whether it is dirty or clean
2. Suck
3. If the location is A, move to B
4. If the location is B, move to A
5. Repeat (go to 1)
This vacuum cleaner agent keeps the two locations clean. So in this respect its performance is no worse than the previous vacuum cleaner we were considering. This new vacuum cleaner, however, unlike the previous one, sometimes engages in what we might regard as wasted action. This vacuum cleaner sucks its current location whether or not the location is dirty.
Does this make the second vacuum cleaner agent less rational than the first? Or should we say that neither vacuum cleaner agent is rational and that both are mere machines?
If we say neither is rational, what are they missing? Beliefs? Goals? What?
The Intelligence of a Rational Agent
What about the intelligence of a rational agent? Can we say what that is?
"Consider the lowly dung beetle. After digging its nest and laying its eggs, it fetches a ball of dung from a nearby heap to plug the entrance. If the ball of dung is removed from its grasp en route, the beetle continues its task and pantomimes plugging the nest with the nonexistent dung ball, never noticing that it is missing. Evolution has built an assumption into the beetle’s behavior, and when it is violated, unsuccessful behavior results. Slightly more intelligent is the sphex wasp. The female sphex will dig a burrow, go out and sting a caterpillar and drag it to the burrow, enter the burrow again to check all is well, drag the caterpillar inside, and lay its eggs. The caterpillar serves as a food source when the eggs hatch. So far so good, but if an entomologist moves the caterpillar a few inches away while the sphex is doing the check, it will revert to the 'drag' step of its plan and will continue the plan without modification, even after dozens of caterpillar-moving interventions. The sphex is unable to learn that its innate plan is failing, and thus will not change it" (Artificial Intelligence. A Modern Approach, 39). Intelligence in a rational agent, it seems, consists in the ability the agent possesses to form beliefs by drawing conclusions in certain circumstances that help it achieve its goals.
An example may make this idea a little clearer.
Consider an agent with a goal to avoid certain things in the environment, say its coming close to a fire. Suppose that this agent forms beliefs about its environment through perception. Suppose, moreover, that at some point this agent observes the presence of smoke in its immediate surroundings. Since this agent observes smoke but does not observe a fire, the observation of smoke itself does not provoke a response. Suppose, however, that the agent has the ability to perceive the presence of smoke and to reason from its observation that there is smoke to the conclusion that a fire is the cause of this smoke. Its ability to form beliefs in this way can help this agent achieve its goals. Further, compared to an agent who lacks this ability to reason to causes from what it observes, this agent clearly seems more intelligent.
The intelligence we can see in the fire example consists in an ability to engage in a certain kind of thinking we might call reasoning. Humans have this intelligence, but they have others too. In this course, we will think about some of them and whether we can use certain techniques in logic to represent them in sufficient detail to implement them on a machine.
This approach to representing some of forms of intelligence that characterize a rational agents requires us to understand certain elementary parts of logic. The understanding we need is the subject of the next lecture, but because this is not a course in logic, we will not worry too much about many of the more technical details that are part of a logic course.
First, though, before we turn to logic, it will be helpful to think more about the observation-thought-decision-action cycle that provides the basic pattern for a rational agent.
The Observation-Thought-Decision-Action Cycle
Our discussion has brought to light what in hindsight should seem obvious:
that rational agents try to determine whether things are to their liking,
try
to make things better if they are not to their liking, and do this in a cycle over and over again throughout their existence.
Zeus makes Sisyphus's "cycle" especially frustrating.
"I saw Sisyphus in violent torment, seeking to raise a monstrous stone with both his hands.
He would brace himself with hands and feet, and thrust the stone toward the crest of a hill,
but as often as he was about to heave it over the top, the weight would turn it back,
and then down again to the plain would come rolling the ruthless stone. But he would strain
again and thrust it back, and the sweat flowed down from his limbs, and dust rose up
from his head"
(Homer, Odyssey XI.593).
The word 'epistemic' is a near transliteration of the Greek
noun ἐπιστήμη (which is often translated into English as 'knowledge.')
In ancient Greek philosophy, the dominant philosophical tradition thought that
knowledge of certain aspects of the world is
necessary for human beings to orient themselves properly and thus for them to live the kind
of lives the ancient philosophers understood as good lives.
The thinking that underlies this cycle falls roughly into two parts with different functions. The aim in one part is to form beliefs about the world. We can call the thinking that discharges this function "epistemic" cognition. The aim in the other part is to evaluate the world as represented by these beliefs, select plans aimed at changing the world, and execute these plans. We can call the thinking that discharges this function "practical" cognition.
All forms of intelligence fit somewhere in this cycle. So, in the fire example we considered, both agents form the belief that there is smoke. This belief is a function of epistemic cognition.
The observation-thought part of the cycle
To get clearer about the cycle, it is necessary to solve several problems.
One of these problems has a traditional name in philosophy. It is called the problem of knowledge.
Rational agents must have the ability to acquire beliefs about themselves and about the environment in which they exist. This is necessary because how the agent acts depends on how it thinks the world is, but the agent cannot form its beliefs randomly.
Their beliefs must have a special property. What property?
For now, we can say that the agent aims for beliefs that constitute "knowledge."
Some knowledge, it seems, may be built into a rational agent, just as in human beings some knowledge might be innate, but in a world with a changing environment, neither a human being nor an artificially rational agent can be equipped from its inception with all the information it needs. Both must acquire new beliefs by sensing its surroundings.
"A computer program capable of acting intelligently in the world must have a general representation of the world in terms of which its inputs are interpreted. Designing such a program requires commitments about what knowledge is and how it is obtained. Thus, some of the major traditional problems of philosophy arise in artificial intelligence" (John McCarthy & Patrick J. Hayes, "Some Philosophical Problems from the Standpoint of Artificial Intelligence," 1969). This may help explain why progress in AI has been slower than some have anticipated. Not all the problems are straightforward engineering problems. The problem of knowledge is an example. No set of procedures for getting information about the environment gives the agent knowledge unless the procedures are for forming and maintaining rational beliefs, and whether a procedure for getting information has this property is at least partly a question in philosophy.
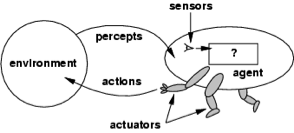
"Logical AI involves representing knowledge of an agent’s world, its goals and the
current situation by sentences in logic. The agent decides what to do by
inferring that a certain action or course of action was appropriate to achieve the goals.
The inference may be monotonic, but the nature of the world and what can be known about
it often requires that the reasoning be nonmonotonic"
(John McCarthy, "Concepts of Logical AI," 2000).
As an example of a way of forming and maintaining beliefs that can constitute knowledge,
consider the way human beings form rational beliefs from their perceptions.
Perception is a process that begins with the stimulation of sensors of some sort and ends with beliefs about immediate surroundings. However all the details in the process from sensation to belief are worked out, it is clear that perception does not always result in true beliefs. A perceptual belief P (where P is a variable that ranges over the beliefs possible given the perceptual apparatus of the agent) is defeasible. That is to say, it is possible for the agent to acquire new information that makes it rational to withdraw the belief it formed from the perception. For example, it is rational for a human agent who sees what looks to be a red object to form the belief that the object is red. Suppose, however, that he becomes aware of the possibility that the light in the circumstances is not normal. Suppose, further, that he believes that light can make an object that is not red appear red. In these circumstances, it is rational for him to retract his belief that the object is red. He need not retract it. He has other options, but retracting the belief in these circumstances is something he is permitted to do.
The decision-action part of the cycle
It is not enough for an agent to observe the world and to form beliefs about it. The agent must act, and some of its actions must be based on the beliefs it formed about how the world is.
Whether the agent likes its situation depends on
what it believes is true of its situation. So one thing an agent can do to make it like
its situation is to change its beliefs. We usually change our beliefs to track changes
in the world, but we can instead use non-rational means to abandon a belief.
Is it rational for an agent to use non-rational means to abandon a belief so that it
likes its situation more?
The answer
may depend on the case.
Some beliefs can make a person extremely miserable, so it might be rational to undergo
hypnosis, say, to get rid of them.
In the case of such actions, the agent will have evaluated the world as represented by its
beliefs. If this evaluation shows that the world is not enough to its liking,
then the agent will typically form and evaluate
plans to make the world more to its liking. On the basis of this evaluation of its plans, the agent
will
select one of the
plans and take steps to execute it.
How does an agent evaluate the world?
Earlier we said that the agent determines whether it likes or dislikes the way the world is.
How does an agent use its likings and dislikings?
The Thought Part of the Cycle
To build our model, then, we face many obstacles.
We need, first of all, to get straight on the beliefs on which the agent relies when it acts.
Must these beliefs be knowledge? Or is it enough that they are rational?
What is knowledge? What is belief?
The questions are philosophical questions. Answers to them are controversial, but it is possible to make some progress by thinking about how we ordinarily use the words know and believe.
If consider how we use the word know in ordinary English language sentences, we can see that sometimes we use it as a propositional attitude verb. The sentence Tom knows that Socrates died in 399 BCE is an example. We also use believe this way. Tom believes that Socrates died in 399 BCE is an example. In these sentences, know and believe are propositional attitude verbs.
To begin to understand what knowledge is and how it differs from belief, we can think about the
difference in the attitudes these two verbs express in these
sentences. In both sentences, the attitude is toward the same proposition: that
Socrates died in 399 BCE.
What propositions are is a difficult issue, but there are straightforward
constructions in English that allow us to talk about them. When we nominalize a declarative sentence,
we form a phrase that can be used as a subject in a sentence. So, for example,
we can nominalize the sentence
"Socrates died in 399 BCE"
to form
the subject "that
Socrates died in 399 BCE."
Now we can say things about
the proposition. We can say
"That
Socrates died in 399 BCE is true"
or
"It is something historians believe is true."
Given this much, we can understand that certain verbs in English are propositional attitude verbs. Examples
are knows, believes, fears, hopes, and so on. We can say of someone that they know that
Socrates died in 399 BCE,
they they believe that Socrates died in 399 BCE, and so on.
Arguments have premises and a conclusion. Declarative sentences express the premises and conclusion. An argument
is valid iff it is impossible for the conclusion to be false if the premises are true. An
argument is sound iff it is valid and its premises are true.
Note that it follows from these definitions that a sound arguments have true conclusions.
This is the proposition Tom is said to know in the first sentence and
to believe in the second. The difference is in the attitude each ascribes to the subject.
The first sentence says that the subject knows the proposition that Socrates died in 399 BCE.
The second says the subject believes the proposition.
It becomes clear, if we think about it, that the two sentences say different things. What someone knows he believes, but what someone believes he does not necessarily know. So, because it possible for Tom to believe but not to know the proposition that Socrates died in 399 BCE, the sentences can have different truth values and thus are not synonymous.
Another way to express this point is in terms of the following arguments:
Knowledge entails Belief
1. Tom knows that Socrates died in 399 BCE
----
2. Tom believes that Socrates died in 399 BCE
Knowledge entails Truth
1. Tom knows that Socrates died in 399 BCE
----
2. Socrates died in 399 BCE
These arguments are valid. In each case, the conclusion cannot be false if the premise is true. The same, however, is not true for the following arguments. They are not valid.
True Belief entails Knowledge
1. Tom believes that Socrates died in 399 BCE
2. Socrates died in 399 BCE
----
3. Tom knows that Socrates died in 399 BCE
Belief entails Truth
1. Tom believes that Socrates died in 399 BCE
----
2. Socrates died in 399 BCE
In each case, it is possible for the premises to be true and the conclusion to be false.
For discussion of knowledge and its philosophical analysis in terms of justification, belief, and truth, see The Analysis of Knowledge in the Stanford Encyclopedia of Philosophy. The first argument is not valid because a true belief need not be knowledge. It is possible that the subject has a true belief but does not have knowledge because his belief is not justified.
Why does "justified" mean here?
Knowledge requires that the subject be a special position with respect to the proposition he knows. Lucky guesses are not knowledge. A standard way in philosophy to express the general point is to say that the agent must have Justified beliefs are rational beliefs. Rational beliefs are the product of correct thinking. They are formed rationally. When we give justification for a belief, we are trying to show that holding the belief is rational. what is called "justification" for the belief.
To understand this, suppose that Tom has the belief on the basis of a dream. In this case, when we think about it, it seems very plausible to say that he does not know that Socrates died in 399 BCE even if this proposition is true. If we ask ourselves why this seems plausible, the reason that comes to mind is that Tom did not form the belief in a correct way. Beliefs about the distant past formed on the basis of a dream are not knowledge even if they happen to be true. If someone questions Tom about why he believes that Socrates died in 399 BCE, he can explain why he has his belief. He would not, however, show he has justification for his belief by saying that he saw Socrates drink the hemlock in a dream. His belief is not knowledge.
The reason that the argument Belief entails Truth is not valid is much more obvious. From the mere fact that Tom has the belief that Socrates died in 399 BCE, it does not at all follow that his belief is true. As we all are very clearly aware, false beliefs (believing a proposition is true when it is not) are exceedingly common. These beliefs, although common, do not count as knowledge. If a proposition I claim to know is false, then my claim to know it is false too.
"Thinking ...
starts with an enormous collection of premises (maybe
millions of them) about a very wide array of subjects" (Levesque, Thinking as Computation, 19).
"[T]hinking means bringing what one knows to bear on what one is doing.
But how does this work? How do concrete, physical entities like people engage with
something formless and abstract like knowledge? What is proposed in this chapter
(via Leibniz [polymath, 1646-1716]) is that people engage with symbolic representations
of that knowledge. In other words, knowledge is represented symbolically as a collection of sentences in a
knowledge base, and then entailments of those sentences are computed as needed" (Levesque, Thinking as Computation, 19).
This makes
thinking presuppose knowledge (and hence beliefs since knowledge entails belief).
Given this, we can
ask whether know is the right word in Levesque's assertion
in Thinking as Computation that
"[t]hinking is bringing to bear what you know on what you are doing"
(3).
Levesque's view is "that thinking is a form of computation," that just as "digital computers perform calculations on representations of numbers, human brains perform calculations on representations of what is known" (2) when we decide what to do.
Is Levesque right? Is knowledge the state in terms of which a rational agent makes decisions?
How do we determine whether Levesque is right?
One way (and perhaps the only way at present) is to consider possible counterexamples.
Suppose, for a possible counterexample, that someone is considering whether to carry an umbrella when he goes out for the day. To decide, he looks out the window. It looks cloudy to him, so he decides to bring an umbrella. In fact, it is not cloudy outside. It looks cloudy to him because the window is painted so that he thinks he sees clouds when he looks outside. Since knowledge entails truth, he believes but does not know that it is cloudy outside.
This"umbrella example seems to show that Levesque is mistaken and that the state the agent uses to represent the world and brings to bear in deciding what to do is belief, not knowledge. The agent thinks it is likely to rain because he believes it is cloudy outside. His belief is false, but it seems perfectly rational. So does his action of carrying an umbrella.
The "Knowledge Base" (KB)
This has implications for the Observation-Thought-Decision-Action Cycle.
Recall that we have said that part of the intelligence of a rational agent consists in acting against the background of a representation of the world. In AI, as we have seen in remarks Levesque makes, it is traditional to call this representation a "knowledge base" (KB) and to suppose that it contains propositions. These propositions are how the world seems to the agent.
The umbrella example shows (or at least seems to show) that the "knowledge base" (KB) in our model of the intelligence of a rational agent should consist in propositions the agent believes. Rational agents represent their circumstances in terms of their beliefs. Some of these beliefs may be knowledge, but the umbrella examples shows they need not all be knowledge.
This, at any rate, will be our assumption in the course until further notice. We will though, to follow tradition, continue to use the term "knowledge base" (KB) in our discussion.
The Computation on the Knowledge Base
In addition to having beliefs, rational agents use their beliefs in thinking about what to do. (We saw an example in the fire example.) The assumption in this course is that this thinking is a computational process. Further, we will try to use what is called backward chaining as a basic part of the algorithm in terms of which we will represent this computational thinking.
"The core idea is that an intelligent agent receives percepts from the external world in the form of
formulae in some logical system (e.g., first-order logic), and infers, on the basis of these percepts
and its knowledge base, what actions should be performed to secure the agent’s goals"
(Stanford Encyclopedia of Philosophy, Artificial Intelligence, 3.2).
We can say that a process is computational iff there is an algorithm to compute it. We know, for
example, that the addition of two integers and certain other mathematical operations on numbers are computational processes
because we know there are algorithms to compute them.
What is an algorithm?
This is a harder question to answer, but here is an easy to understand example for addition. Suppose we represent numbers with
hash marks, so | for 1, || for 2, and so on. Then concatenation is an algorithm we can use to
compute addition.
To determine what number | + || is, we know what to do. We concatenate | and || to make |||.
This raises a host of questions.
What is a computation?
Computations operate on symbolic structures.
What is a symbolic structure?
The agent's beliefs are propositions in its "knowledge base" (KB). These propositions are sentences in a formal language. In AI, this formal language is traditionally the language of the first-order predicate calculus. The sentences in this formal language are symbolic structures. (We will consider these structures in more detail in the next lecture.)
What is the operation or operations in the computations on these symbolic structures?
"[L]ogic programming ... is the most widely
used form of automated reasoning" (Stuart Russell & Peter
Norvig Artificial Intelligence, A
Modern Approach, 337).
This approach to AI is sometimes called "logic-based AI" (Stanford Encyclopedia of Philosophy,
Artificial Intelligence).
In the logic programming/agent model, backward chaining is the fundamental operation.
What does this operation do?
Levesque (in 2.2 of
Thinking as Computation) talks about computing "logical entailment" (24).
For now, it is not necessary to worry about the difference between logical consequence and logical entailment.
We will consider the difference in more detail in the next lecture.
It computes logical consequence.
What is logical consequence? How does backward chaining compute logical consequence?
These questions take some time to answer. For now, we will consider an example.
Backward Chaining on the KB
One way to think about backward chaining goes all the way back to Aristotle (385-322 BCE). He observed that deliberation about how to satisfy a goal is a matter of working backwards in thought from the goal to something the person takes themself to be able to do. Aristotle's idea, roughly, is that as part of having reason, human beings form goals for the things they believe are good. Further, in order to take action, they deliberate about what to do to achieve these goods in the circumstances in which they find themselves. Deliberation, in this way, is a "goal-reduction procedure." It is procedure to reduce the goal to something one can do.
A simple example helps illustrate backward chaining in a goal-reduction procedure.
For the example, suppose that there are basic actions. These are actions someone can do without doing something else. Lifting my right arm above my head might be an example. I can lift my right arm above my head, and I can do it without doing anything else. Because my right arm is not impaired in any way, I do not have to use something, say my left arm, to raise my right arm over my head. Opening a door is not a basic action for me. I can open a door, but I have to do it by doing several other more basic things. I have to grab the knob, twist, and pull the door open. So, in order to open the door, I do several other things. That is to say, for it to be true that I open the door, it has to be true that I grab the knob, twist, and pull open the door.
This general idea may be reflected formally. A formula of the form
a ← b, c.
understood to say that for a to be true, it is sufficient for b and c to be true. By contrast,
d.
says simply that d is true. There is no backward arrow (←) in this second formula. This formula says simply that d is true (and not that d is true if b and c are true).
Now, given this explanation of the
two formulas, suppose that an agent has beliefs (or perhaps knowledge) about
the conditions sufficient for various possible actions it can perform. Suppose that these beliefs are
in the
knowledge base or KB for the agent. In the context of
Why is the KB called a program? The idea is that given an input, the KB can be "run" in order
to produce an output. The input to the KB is called a query. Backward chaining
occurs when the KB is
run with this input. The output is positive if the input is a logical consequence
of the KB.
This will become clearer in the next lecture.
logic programming, this KB for the agent is called a "logic program":
a ← b, c. " a is true if b and c true are true"
a ← f.
b. " b is true"
b ← g.
c.
d.
e.
Here is a more formal description of the backward chaining that occurs in example. a is the query. It is posed to the KB. To answer the question of whether the query is a logical consequence of the KB, backward chaining occurs. The first step in the algorithm is to determine whether the query matches a head of one of the formulas in the KB. Given the KB in the example, the query matches the head of the first formula in the KB. (a is the head in the formula a ← b, c. The tail is b, c.) Given this match, backward chaining now issues in two derived queries, b and c. (The tail provides the derived queries.) These queries are processed last in, first out (LIFO). b matches the head of the third formula in the KB. There is no derived query. The remaining query is c. It matches the head of the fifth formula. There is no derived query. Now there are no more queries to process, so backward chaining stops and a positive answer is returned to the query: a is a logical consequence of the KB. If an agent with this KB asks itself whether "a is true," backward chaining supplies the answer. The goal a reduces to two subgoals (b and c), and these subgoals are true in the KB.
An Example in Prolog Notation
Prolog is a
computer programming language we will occasionally use in
this course. We will consider how Prolog works in more detail in the next lecture. Our goal, though,
is not to be become Prolog programmers. This is a course in philosophy, not a course in computer science.
We consider Prolog only to show how one form of intelligence (computing logical consequence) in a rational
agent can
be implemented on a machine.
Here is a (slightly more complicated and abstract) goal-reduction example in Prolog notation.
Suppose the query
?- a, d, e.
is put to the following KB and what is also called a program:
a:-b, c. (this is Prolog notation for "a ← b, c.")
a:-f.
b.
b:-g.
c.
d.
e.
f.
There are three possible computations given the query. These computations may be understood in terms of the following (upside down) tree whose nodes are the query lists. The commentary describes the computation represented in the the leftmost branch of the tree.
?- a, d, e.
The initial query list is a, d, e. This list is processed
last in, first out. The last query pushed onto the list is a. To
process a, the KB is searched top-down for a match with the
head of one of the clauses. a matches the head of first rule a:-b, c.
The tail (b, c) is pushed on to the query list. Now this
query list (b, c, d, e) is processed again.
|
/ \
?- b, c, d, e. ?- f, d, e.
b matches a fact (b) in the KB.
Facts have no tail, so nothing is
pushed onto the query list.
| |
/ \
?-c, d, e. ?-g, c, d, e. ?- d, e.
c matches a fact.
| | |
?- d, e. • ?- e.
d matches a fact.
| |
?- e. ⊥
e matches a fact.
The query list is now empty.
|
⊥
The computation stops. The
initial query is successful.
a, d, and e are logical
consequences of the KB.
Each branch is a computation. Backward chaining constructs them one at a time. The left most branch is successful. It finds that a, d, e is a consequence of the KB. More computation to answer the initial query is not necessary, but for illustration I have represented in the tree.
This tree raises several questions.
For now, just make sure you understand how to do the computations.
In the next lecture, we will consider in more detail how the backward chaining algorithm (the steps in the computation) computes logical consequence, what logical consequence is, and how the intelligence backward chaining implements functions in our model of a rational agent.
The London Underground Example
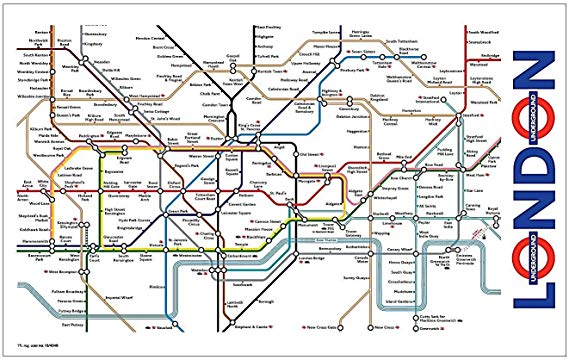 The above examples are artificial, but there are real world examples.
The above examples are artificial, but there are real world examples.
Consider the "London Underground" example Robert Kowalski discusses (in Chapter 1 of Computational Logic and Human Thinking, 24). The instructions in the emergency notice in the London Underground can be understood to include a goal-reduction procedure. In the instructions of what to do in case of an emergency, the first sentence
Press the alarm signal button to alert the driver
can be understood as saying that
the goal of alerting the driver reduces to the subgoal of pressing the alarm signal button
We will
talk more about maintenance goals later in the course--for now it is enough know that they
will be an important part of what we are calling the logic programming/agent model.
If the typical passenger has the "maintenance goal"
If there is an emergency, then I deal with the emergency appropriately
and has the beliefs
I deal with the emergency appropriately
if I get help
I get help if I alert the driver
then the instructions in the London Underground may be incorporated into the agent's mind in the form of a logic program (in which the beliefs constitute the KB).
This program functions as the "knowledge" the agent brings to bear on the situation. If the agent observes an emergency, his observation will trigger the antecedent
there is an emergency
of his or her maintenance goal
If there is an emergency, then I deal with the emergency appropriately
We will talk more about achievement goals later in the course. Here we are giving them as queries to the KB. This in turn gives the agent a goal to achieve, an achievement goal. It is
I deal with emergency appropriately
To achieve this goal, backward chaining reduces the goal an appropriate subgoal. So, given the beliefs in the KB, backward chaining results in a plan of action
I alert the driver.
A Dual Process Model of Human Thinking
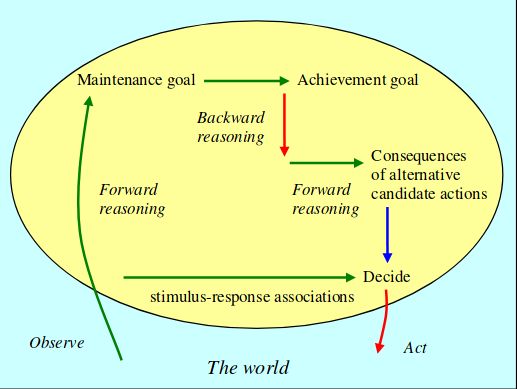 It seems obvious that human beings do not always explicitly reason in the way set out
in the "London Underground" example, and of course Kowalski does not think otherwise.
His view, as I understand it,
is that human beings sometimes do reason explicitly in this way but that they also perhaps more frequently
employ what he calls "intuitive
thinking."
It seems obvious that human beings do not always explicitly reason in the way set out
in the "London Underground" example, and of course Kowalski does not think otherwise.
His view, as I understand it,
is that human beings sometimes do reason explicitly in this way but that they also perhaps more frequently
employ what he calls "intuitive
thinking."
Kowalski shows what he calls "deliberative thinking" in the top of the circle that represents the "mind." He
shows what he calls "intuitive thinking" at the bottom.
"[I]n recent years, cognitive psychologists have developed Dual Process
theories, which can be understood as combining descriptive and normative theories.
Viewed from the perspective of Dual Process theories, traditional descriptive
theories focus on intuitive thinking, which is associative, automatic, parallel
and subconscious. Traditional normative theories, on the other hand, focus on deliberative thinking,
which is rule-based, effortful, serial and conscious. In this book,
I will argue that Computational Logic is a dual process theory, in which intuitive and
deliberative thinking are combined" (Kowalski, Computational Logic and Human Thinking, 15).
These "dual process theories" to which Kowalski refers are probably necessary for understanding rationality in human beings, but we will not much consider them. In this course, our aim is much more modest. We are not trying to do cognitive science. We are trying to take some very beginning steps to make a model of a (not very intelligent) rational agent.
What we have Accomplished in this Lecture
We have constructed a very simple and clearly incomplete model of the intelligence of a rational agent. Rational agents have beliefs about the world, and they reason in terms of these beliefs to decide what to do in order to satisfy their goals. The KB or logic program is a symbolic structure that represents the agent's beliefs. The backward chaining algorithm on the KB implements the agent's thinking about logical consequences of its beliefs.

