Philosophy, Computing, and Artificial Intelligence

⊕ "A common misconception about reasoning is that reasoning is deducing, and in good reasoning the conclusions follow logically from the premises. It is now generally recognized both in philosophy and in AI that nondeductive reasoning is at least as common as deductive reasoning, and a reasonable epistemology must accommodate both. For instance, inductive reasoning is not deductive, and in perception, when one judges the color of something on the basis of how it looks to him, he is not reasoning deductively. Such reasoning is defeasible, in the sense that the premises taken by themselves may justify us in accepting the conclusion, but when additional information is added, that conclusion may no longer be justified. For example, some thing’s looking red to me may justify me in believing that it is red, but if I subsequently learn that the object is illuminated by red lights and I know that that can make things look red when they are not, then I cease to be justified in believing that the object is red" (John L. Pollock, "Defeasible Reasoning." Cognitive Science, 11, 1987, 481-518).

"We can combine all of a cognizer’s reasoning into a single inference graph and regard that as a representation of those aspects of his cognitive state that pertain to reasoning. The hardest problem in a theory of defeasible reasoning is to give a precise account of how the structure of the cognizer’s inference graph determines what he should believe. Such an account is called a 'semantics' for defeasible reasoning, although it is not a semantics in the same sense as, for example, a semantics for first-order logic. If a cognizer reasoned only deductively, it would be easy to provide an account of what he should believe. In that case, a cognizer should believe all and only the conclusions of his arguments (assuming that the premises are somehow initially justified). However, if an agent reasons defeasibly, then the conclusions of some of his arguments may be defeaters for other arguments, and so he should not believe the conclusions of all of them. ... We want a general account of how it is determined which conclusions should be believed, or to use philosophical parlance, which conclusions are “justified” and which are not. This distinction enforces a further distinction between beliefs and conclusions. When a cognizer constructs an argument, he entertains the conclusion and he entertains the propositions comprising the intervening steps, but he need not believe them. Constructing arguments is one thing. Deciding which conclusions to accept is another" (John L. Pollock, "A Recursive Semantics for Defeasible Reasoning." Argumentation in Artificial Intelligence, edited by Guillermo Simari and Iyad Rahwan (Springer, 2009), 173-197). In an environment of real-world complexity, rational agents must be able to form beliefs and make decisions against a background of pervasive ignorance. Because this is unavoidable, rational agents cannot be confined to logical deductions. They must sometimes reason defeasibly and thus withdraw their conclusions when they acquire new information.

It seems true that the justification necessary for belief seems to depend on the importance of the matter to the agent. As the importance increases, the evidence necessary for belief increases. So rational agents must also be capable of changing their beliefs as the importance changes.

Even with NAF, the logic programming/agent model accounts for neither of these facts.

Beliefs and Defeasible Reasoning

We can represent defeasible reasoning in terms of arguments that have two kinds of defeaters.

One kind of defeater is a rebutting defeater. It attacks the argument by attacking its conclusion and so provides a reason to think the conclusion of the argument is false.

The other kind of defeater is an undercutting defeater. It attacks the argument by providing a reason to think that the premises do not provide a reason to think the conclusion is true.

John Pollock (who did some the fundamental work on defeasible reasoning) gives this example:

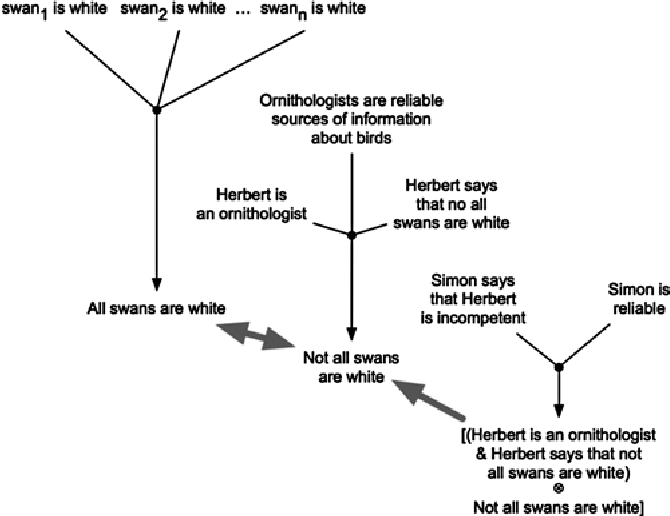
Argument 1 is the argument on the left in the graph. The agent observes n white swans. These observations give the agent beliefs he uses as premises ("swan 1 is white," and so on) in an argument that provides a defeasible reason for him to believe that all swans are white.

In Argument 2, an ornithologist (Herbert) informs the agent that not all swans are white. Since the agent bellieves that ornithologists are reliable sources of information about birds, ⊕ the agent has an argument that provides him with a defeasible reason to believe that not all swans are white. This conclusion in Argument 2 rebuts the conclusion of Argument 1. ⊕

In Argument 3, Simon (whom the agent believes is reliable) says that Herbert (the ornithologist) is incompetent. This argument (that Herbert is incompetent because Simon is reliable and says that Herbert is incompeent) undercuts the conclusion in Argument 2.

⊕ "What will prove to be a pivotal observation is that, at least in humans, the computation of defeat statuses, and more generally the computation of degrees of justification, is a subdoxastic process. That is, we do not reason explicitly about how to assign defeat statuses or degree of justification to conclusions. Rather, there is a computational process going on in the background that simply assigns degrees of justification as our reasoning proceeds. If we knew how to perform this computation by explicitly reasoning about inference-graphs and degrees of justification, that would make it easier to find a theory that correctly describes how the computation works. But instead, the computation of degrees of justification is done without our having an explicit awareness of anything but its result. Similar subdoxastic processes occur in many parts of human cognition. For example, the output of the human visual system is a percept, already parsed into lines, edges, corners, objects, etc. The input is a time course of retinal stimulation. But we cannot introspect how the computation of the percept works. To us, it is a black box. Similarly, the process of computing degrees of justification is a black box that operates in the background as we construct arguments in the foreground. Two important characteristics of such background computations are, first, that the output has to be computable on the basis of the input, and second, that the computation has to be fast. In the case of vision, the computation of the percept takes roughly 500 milliseconds. If it took longer, in many cases vision would not apprise us of our surroundings quickly enough for us to react to them. Similarly, degrees of justification must be computable on the basis of readily observable features of conclusions and their place in the agent's inference-graph. And the computational complexity of the computation must be such that the computation can keep up with the process of constructing arguments. As we will see, these simple observations impose serious restrictions on what theories of defeasible reasoning might be correct as descriptions of human reasoning..." (John L. Pollock, "Defeasible Reasoning and Degrees of Justification." Argument & Computation, 1:1, 2010, 7-22). Given these three arguments, what is the agent permitted to believe?

Is the agent permitted to believe that all swans are white (the conclusion in Argument 1?

The answer, it seems, is "yes."

Why?

Argument 2 attacks Argument 1 by rebutting its conclusion. Argument 3 attacks Argument 2 by undercutting its conclusion. Thus Argument 1 remains undefeated.

Argumentation Semantics

We can set out the procedure to compute defeat more formally.

<Arg, Att> is an argumentation framework. Arg is a set of arguments. Att is a subset of Arg x Arg. Att encodes the attack relations between the arguments in Arg. Argument A attacks argument B just in case <A, B> is in Att.

An example makes it a little clearer how this works.

Suppose there are three arguments, A, B, and C. Suppose that B attacks A and that C attacks B. These relationships among the arguments may be pictured as follows:

A <---- B   (A is attacked by B)     B <---- C   (B is attacked by C)

Given this argumentation framework, what conclusions is the agent permitted to believe?

The answer, it seems, is that the agent is permitted to believe the conclusions of A and C.

Why?

Argument B attacks argument A, but argument C attacks argument B. Further, no argument attacks argument C. So, in the KB, arguments A and C remain undefeated.

A procedure to determine which conclusions an agent is permitted to believe is an argumentation semantics. The semantics we are using works in terms of three conditions:

• An argument is in (or undefeated) iff all its attackers are out.
•An argument is out (or defeated) iff it has at least one attacker that is in.
•An argument is undecided iff it is neither in nor out.

In the example, Arg = {A,B,C} and Att = {<B, A>, <C,B>}.

C is in because all its attackers are out. (All of C's attackers are out because C has no attackers.)

C attacks B, and C is in. Therefore, B is out.

A is in because all its attackers are out. (All of A's attackers are out because A has no attackers.)

⊕ Richard Nixon was the 37th President of the United States. As a boy, he went to Quaker meetings and played the piano at services. In politics, he was a hawk on the war in Vietnam. In the presidential election of 1972, he won in a landslide against Democratic Senator George McGovern McGovern was calling for an immediate end to the war. Here is another example, commonly referred to as the "Nixon Diamond."

There are two arguments:

Argument A:
Nixon is a Quaker. Therefore, he is against the war in Vietnam.

Argument B:
Nixon is a Republican. Therefore, he is for the war in Vietnam.

The argumentation framework is <Arg, Att>, where

Arg = {A, B} and Att = {<A, B>, <B, A>}.

This framework gets its name because it was originally depicted as follows:

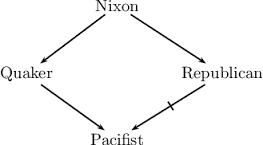
The attack relations between the arguments A and B are

A <---- B   (A is attacked by B)     B <---- A   (B is attacked by A)

Given the argumentation framework, there are three possible complete labellings:

1. A = in, B = out
2. A = out, B = in
3. A = undecided, B = undecided

Which labelling is correct?

The answer, it seems, is that the third is correct.

It is not rational for the agent to accept the conclusion of either argument A or argument B.

Degree of Justification and Degree of Importance

The degree of justification necessary for belief seems to vary with degree of importance. ⊕ "The practical importance of a question (i.e., our degree of interest in it) determines how justified we must be in an answer before we can rest content with that answer. For example, consider a ship's captain on a busman's holiday" (John L. Pollock, Cognitive Carpentry. A Blueprint for How to Build a Person, 48. MIT Press, 1995).

"[T]here is a difference between a conclusion being 'justified simpliciter' and having a degree of justification greater than 0. Justification simpliciter requires the degree of justification to pass a threshold, but the threshold is contextually determined and not fixed by logic alone" (John L. Pollock, "Defeasible Reasoning and Degrees of Justification." Argument & Computation, 1:1, 2010, 7-22).

"[N]otice that beliefs and probabilities play different roles in decision-theoretic reasoning. Beliefs frame the problem, providing the background against which we compute probabilities and expected-values and make our decisions. For example, suppose you are in San Francisco and you about to drive over the Golden Gate Bridge in order to visit Pt. Reyes National Seashore. In making the decision to take this little vacation trip, you consider how much it is apt to cost, how much time it is apt to take, how much pleasure you expect to derive from it, and so forth. These are all assigned probabilities. But you take it for granted that the bridge will not collapse while you are driving over it. You do not assign a probability to that. If you did assign a probability to the bridge collapsing, and it were greater than 0, then no rational person would make the trip, because no matter how improbable a bridge collapse is, dying because you are on a collapsing bridge more than outweighs whatever pleasure you may get from visiting the sea shore, and so the expected-value of making the trip would be negative. It can only be reasonable to make such a trip if you take the probability of a bridge collapse to be 0. Similarly, when you fly to a conference, you simply believe that the airplane will not crash. Unless you assigned that probability 1, the expected-value of going to the conference would be negative, no matter how good the conference. All decision problems are framed against a background of assumptions that you simply believe outright, and you take yourself to be fully justified in believing them. You do not assign probabilities to these beliefs when computing expected-values, or if you do, you assign them probability 1" (John Pollock, "Problems for Bayesian Epistemology," 12). To see that this is true, consider Pollock's example of the ship captain on a "busman's holiday."

The ship captain is on a cruise vacation (and hence Pollock's description of the captain as on a "busman's holiday"). At first, he is a passenger on the cruise ship and has no other role. He wonders how many lifeboats are onboard. Pollock says that "[t]o answer this question, he might simply consult the descriptive brochure passed out to all the passengers."

Now the captain's circumstances change.

The ship is in danger of sinking because there has been an accident. The ship's officers, in including its captain, are incapacitated. The vacationing captain becomes aware of the situation and assumes command. In his new circumstances, he cannot rely on the brochure for the number of lifeboats. Pollock says that "it becomes very important for him to know whether there are enough lifeboats" and that the captain "must either count them himself or have them counted by someone he regards as reliable" because now "[t]he importance of the question makes it incumbent on him to have a very good reason for his believed answer."

Change in the Degree of Importance

As a passenger on a vacation, the number of lifeboats is not very important to the captain. What he needs to decide is where to eat, which shows to attend, and so on. For these decisions, the number of lifeboats does not matter. Its degree of importance is low enough that the degree of justification required to "rest content" with an answer is minimal. The captain, then, can form a belief on the basis of the brochure, and he can frame his decision problems this way when he is considering where to eat and so on. He can treat the number of lifeboats, whatever the brochure says it is, as part of the description of how the world is.

After the accident, the number of lifeboats matters much more to the captain. Unless he can increase his degree of justification by counting them or by having someone reliable count them for him, when he is thinking about what to do, he will have to treat the brochure as making it only probable that the number of life boats is what the brochure says it is. When, for example, he is deciding whether to give the order to abandon ship to wait in the lifeboats for rescue, he will not be able treat the number of lifeboats as part of how the world is. To make his decision, the captain will have to take into account his uncertainty about the number.

What the Captain Knows and When he Knows it

⊕

"We do not ordinarily require of someone who claims to know that he should have the kind of reason and justification for his belief which allows him to rule out all incompatible beliefs, that knowledge has to be firm or certain exactly in the sense that somebody who really knows cannot be argued our of his belief on the basis of assumptions incompatible with it. It seems ordinarily we only expect satisfaction of these standards to the extent and degree which is proportional to the importance we attribute to the matter in question. And thus, following common usage, a skeptic might well be moved to say, in perfect consistency with his skepticism, that he knows this or that. There is no reason that the skeptic should not follow the common custom to mark the fact that he is saying what he is saying having given the matter appropriate consideration in the way one ordinarily goes about doing this, by using the verb 'to know'" (Michael Frede, "The Skeptic's Two Kinds of Assent and the Question of the Possibility of Knowledge," 211. Essays in Ancient Philosophy, Michael Frede (University of Minnesota Press, 1987), 201-222). Suppose that when the captain first boards the ship and wonders about the number of lifeboats, he consults the brochure and comes to believe that there are n lifeboats on the ship. Suppose that the brochure is correct. Does the captain know that there are n lifeboats on the ship?

If knowledge requires the captain to give the matter appropriate consideration relative to its importance, it seems that he does indeed knowem> there are n lifeboats on the ship.

After the accident, Pollock's view seems to be that that the captain does not know. Pollock says that "it becomes very important for him to know whether there are enough lifeboats."

This seems right to me.

The importance the captain attributes to the matter is now much higher. Consulting the brochure is no longer enough justification. The captain should retract his belief.

What we have Accomplished in this Lecture

To get a clearer understanding of the intelligence that characterizes a rational agent, we did three things in this lecture. We considered defeasible reasoning and the conditions under which a rational agent is permitted to believe in the conclusion of an argument. We looked at argumentation semantics for understanding and answering this question. We considered degrees of justification and degrees of importance in connection with knowledge.