Philosophy, Computing, and Artificial Intelligence

Computational Logic and Human Thinking
Chapter 5 (75-91), Appendix A4 (284-289)

Negation-as-Failure and Negation-Introduction

Kowalski describes negation-as-failure (NAF) as the "derivation of negative conclusions from the lack of positive information" (Computational Logic and Human Thinking, 78). This reasoning is defeasible. If we later get positive information, we retract the negative conclusion.

NAF is not reasoning in accordance with the rule of Negation-Introduction (¬I). ⊕ Negation-Introduction (¬I) is a traditional rule of logic.

The rule of Negation-Introduction (¬I) says that if absurdity (⊥) is a logical consequence of a set of premises and assumption φ, then ¬φ is a logical consequence of these premises:

    [φ]¹
      .
      .
      .
     ⊥
  ------- ¬I,1
    ¬φ 

Reasoning in accordance with Negation-Introducion (¬I) is conclusive reasoning. If I get new information that makes it rational for me to retract ¬φ, I will have to retract one of the premises in the argument absurdity (⊥) is a logical consequence of this set of premises.

NAF in Everyday Reasoning

In everyday life, we often reason in the following way.

I look at a schedule of flights from Phoenix to San Francisco. I don't see one listed as leaving at 10:00 am. So I conclude that no flight leaves at that time. This inference seems entirely reasonable, but it is not sanctioned by the classical Negation-Introduction rule.

My reasoning in this example is NAF reasoning. I look to see if a flight is listed as leaving at 10:00 am. This looking results in what Kowalski describes as a "lack of positive information." I don't see a flight listed, so I draw what he describes as a "negative conclusion."

Why NAF Reasoning is Rational

⊕ "The derivation of negative conclusions from the lack of positive information about a predicate is justified by a belief or assumption that we have all the positive information that there is to be had about the predicate" (Kowalksi, Computational Logic and Human Thinking, 78).

"The use of negation as failure to derive a negative conclusion is justified by the closed world assumption that you have complete knowledge about all the conditions under which the positive conclusion holds" (Kowalksi, Computational Logic and Human Thinking, 79). Since NAF reasoning is not conclusive, one might wonder why is it is rational.

One answer is that the agent believes that if a proposition is not a logical consequence of his beliefs, then the proposition is false. This is the closed world assumption (CWA).

Is the CWA reasonable for an agent to believe?

I don't think so. It is not a logical consequence of my beliefs that right now there is a hummingbird at the feeder, but it would be rash for me to conclude that there is not one there. They come and go all day long, so for all I know there might be one there now.

There is another problem too.

Suppose, to use Kowalski's words, that I believe that I "have all the positive information that there is to be had about the predicate." With respect to the flight example, this seems to mean that I believe I know all the flight times from Phoenix to San Francisco. I think, for example, that it leaves once a day at 9:00 am and that it departs at no other time. In this, when I conclude that no flight leaves at 10:00 am, my reasoning is not defeasible. It is conclusive.

Why?

Because if new information makes it rational for me to withdraw my negative conclusion, I would have to withdraw one of the preimses from which I derived this conclusion.

NAF in Default Reasoning

⊕ "[T]he kind of reasoning involved in the suppression task, once its intended logical form has been identified, is a form of default (or defeasible) reasoning, in which the conclusion of a rule is deemed to hold by default, but is subsequently withdrawn (or suppressed) when additional information contradicting the application of the rule is given later" (Kowalksi, Computational Logic and Human Thinking, 48).

"This property of negation as failure and the closed world assumption is called defeasibility or non-monotonicity. It is a form of default reasoning, in which an agent jumps to a conclusion, but then withdraws the conclusion given new information that leads to the contrary of the conclusion" (Kowalksi, Computational Logic and Human Thinking, 81). NAF reasoning is part of what Kowalski calls default reasoning.

This is reasoning "in which the conclusion of a rule is deemed to hold by default, but is subsequently withdrawn (or suppressed) when additional information contradicting the application of the rule is given later" (Computational Logic and Human Thinking, 48).

To see how NAF is part of this reasoning, consider a slight variation on Kowalski's "innocent unless proven guilty" example (Computational Logic and Human Thinking, 84).

(k1) A person is innocent of a crime
if the person is accused of the crime
and it is not the case that the person committed the crime.

(k2) A person committed a crime if another person witnessed the person commit the crime.

(k3) Bob is accused of the crime of robbing a bank

Suppose we think of this example along the lines of a logic program. Suppose the query is

(q) Bob is innocent of the crime of robbing a bank.

Given the first rule (k1) in the KB, this query will succeed if the derived queries succeed:

(i) Bob is accused of the crime of robbing a bank
(ii) It is not the case that Bob committed (the crime of) robbing a bank

To deal with (ii), we have to change how we are understanding backward chaining. We have to incorporate NAF reasoning and understand (ii) to succeed just in case

(*) Bob committed (the crime of) robbing a bank

fails. If we do this, (ii) will succeed and so the original query (q) will succeed too. The agent, in this case, can conclude that Bob is innocent because there is no proof of (*).

Notice that (ii) will not succeed if we change the KB so that it includes the new belief that

Another person witnessed Bob commit (the crime of) robbing a bank

With this new information, (ii) will fail and so the original query (q) will also fail now.

Negation-as-Failure in Logic Programming

Logic programming can be developed in this way so that it allows for NAF.

Logic programs, as we have defined them, do not contain "nots" in the tails of rules. So the first step is to allow for this. We allow a rule to have "nots" in its tail and thus to have the form

positive condition if positive conditions and not-conditions

In addition to this change, we modify the backward chaining computation so that there is a procedure to handle the "nots" that may appear in the tails of the rules in the logic program.

To understand the modification, consider the following logic program with NAF:

P if Q, not-R
R if S, T
Q
S

Relative to this KB, suppose the query is

?-P

This query unifies with the head of the first rule. So the derived query list becomes

Q, not-R

To process the derived query list, we proceed as we did without NAF. We see whether Q unifies with the head of any entry in the KB. It does. It unifies with the first fact in the KB. Since facts have no tail, there is nothing to push onto the derived query list. Now the list

not-R

It is here that we proceed in a way we did not previously. We do not determine whether not-R unifies with the head any entry in the KB. (not-R will not unify with any head in the KB because we do not allow negations in heads of rules.) Instead, in logic programming with NAF, we understand the query not-R to succeed just in case the query

R

fails. To determine is whether R fails, we evaluate R just as we would in logic programming without NAF. We determine whether it unifies with a head of a rule. It does. R unifies with the head of the second rule. So we push the tail of this rule onto the derived query list

S, T

Now we have to process the entries on this derived query list. We process this list as stack, last-in first-out (LIFO). We see that S (the last in and thus the first out) unifies with the head of the second fact. Since facts have no tail, the new derived query list is

T

We see that T does not unify with any head in the program. So now we know that it fails and thus that R fails. So not-R succeeds. Since, as we have seen Q succeeds, it follows that

?- P

succeeds. Hence, P is a consequence (but not a logical consequence) of the program.

The Suppression Task Revisited

In everyday conversation it is common to state only the most important conditions of a general statement and to leave implicit the other conditions that apply.

In the Byrne Suppression Task, the general statement is

If she has an essay to write, she will study late in the library.

If, according to Kowalski (Computational Logic and Human Thinking, 86), the underlying rule in this statement were made more explicit, it would look something like this:

If she has an essay to write,
and it is not the case that she is prevented from studying late in the library,
then she will study late in the library.

To set out this more formally, let the sentences be symbolized as follows:

E = She has an essay to write
L = She will study late in the library
P = She is prevented from studying late in the library

The corresponding logic program or KB with NAF is

L if E, not-P
E

Relative to this KB, the query

?- L

succeeds. This is the outcome the experimenters expect.

Here the computation. L unifies with the head of the rule. The new query list is E, not-P. E unifies with the head of the fact. Facts have no tails. So now the query list is

not-P

To process not-P, we use the negation-as-failure procedure. So not-P succeeds if P fails. Since P does fail, it follows that not-P succeeds. At this point, because the query list is empty, the computation stops. L is a consequence (but not a logical consequence) of the program.

Explaining the Experimental Results

Given NAF and this new KB, it may seem that the logic programming/agent model provides a good way to explain why subjects in the Byrne Suppression Task draw the conclusion

She will study late in the library

on the basis of the premises

If she has an essay to write, then she will study late in the library
She has an essay to write

The subjects incorporate the conditional into their minds in a way that includes

it is not the case that she is prevented from studying late in the library

Since the negation in this "preventing" clause is negation-as-failure, the conclusion L is a consequence (but not a logical conseqence) of the premises in the KB.

This would explain the first experimental result in the Byrne Suppression Task.

It remains, though, to explain the second result. In the Byrne Suppression Task, about 40% of the subjects retract (or "suppress") L upon receiving the new information

If the library is open, she will study late in the library.

To explain this, there must be a natural way to incorporate this new information so that

?- L.

failes. Otherwise, Kowalski has not explained the experimental results in the Suppression Task.

One Way to Incorporate the New Information

It is plausible to think that the new information makes explicit the following preventing condition that was implicit in the original information:

She is prevented from studying late in the library if the library is not open.

When the subjects get this new information, they must incorporate it in their minds. One way to incorporate this new information changes the KB so that it becomes

L if E, not-P
If she has an essay to write,
and it is not the case that she is prevented from studying late in the library,
then she will study late in the library.

P if not-O
She is prevented from studying late in the library if the library is not open.

E
She has an essay to write

L is not a consequence of this KB. So we might conclude that this is the way to incorporate the new information and thus to explain the "suppression" in the Byrne Suppression Task.

Here is the computation that shows L is not a consequence of this KB. The query

?-L

unifies with the head of the first rule. The derived query list is

E, not-P.

E unifies with the head of the fact. It has no tail. So now the derived query list is

not-P

P unifies with the head of the second rule. This produces the derived query

not-O

O does not unify with any head in the KB. So not-O succeeds. This means that not-P fails and hence L fails too. Thus, L is not a consequence (logical or otherwise) of the KB.

A Question about this way of Incorporating the New Information

Does this way of changing the KB explain why subjects "suppress" the conclusion L?

The answer, it seems, is that it does not.

There are lots of possible conditions that would prevent one from studying in the library. Here the possibilities that Kowalski gives (Computational Logic and Human Thinking, 86-87):

She is prevented from studying late in the library if the library is not open.
She is prevented from studying late in the library if she is unwell.
She is prevented from studying late in the library if she has a more important meeting.
She is prevented from studying late in the library if she has been distracted.

In this list, it is not obvious that all of the preventing conditions are negative. So given the new information, it is unclear that the query L to the new KB will always fail.

Hence, it is unclear that Kowalski has provided a general explanation for why subjects in the experiment "suppress" their original conclusion when they receive new information.

Two Other Ways to Incorporate the New Information

Here is the KB before the subject in the Bryne Suppression Task recieves the new information:

E = She has an essay to write
L = She will study late in the library
P = She is prevented from studying in the library

L if E, not-P
E

The query L succeeds in this KB.

Here is one first way to incorporate the new information:

E = She has an essay to write
L = She will study late in the library
P = She is prevented from studying late in the library
C = The library is closed

L if E, not-P
E
P if C
C

Here is another way to incorporate the new information:

E = She has an essay to write
L = She will study late in the library
O = The library is open

L if E, O
E

The query L fails in both of these new KBs.

Which is the more plausible way to incorporate the new information?

The first can seem to be the more plausible of the two insofar as the new information is added without changing or eliminating an entry in the KB. The problem, though, is that there appears to be no justification for adding C (the belief that the library is closed) to the KB.

Kowalski Thinks that the Second Way is Correct

Which of the ways, if either, does Kowalski intend in his explanation of the Suppression Task?

His discussion of the example (Computational Logic and Human Thinking, 86-87) suggests that he thinks that the second way is correct. He says that the "higher-level representation"

she will study late in the library if she has an essay to write and it is not the case that she is prevented from studying late in the library.
she is prevented from studying late in the library if the library is not open.
she is prevented from studying late in the library if she is unwell.
she is prevented from studying late in the library if she has a more important meeting.
she is prevented from studying late in the library if she has been distracted.

⊕ "The relationship between the two formulations [in the Suppression Task] is another example of the relationship between a higher-level and lower-level representation, which is a recurrent theme in this book. In this case, the higher-level rule acts as a simple first approximation to the more complicated rule. In most cases, when a concept is under development, the complicated rule doesn’t even exist, and the higher-level representation as a rule and exceptions makes it easier to develop the more complex representation by successive approximation" (Robert Kowalski, Computational Logic and Human Thinking, 87). is "compiled into" the following "lower-level representation":

she will study late in the library
if she has an essay to write
and the library is open
and she is not unwell
and she doesn’t have a more important meeting
and she hasn’t been distracted.

Kowalski thinks this "compiling" of the "higher" into the "lower-level representation" happens naturally as we gain a more detailed understanding of "she will study late in the library."

This idea of "concept development" (as he calls it in the side note) is interesting and has some initial plausibility, but more explanation is necessary before we can conclude that Kowalski has provided a satisfactory explanation of the experimental results in the Byrne Suppression Task.

Problems for the Logic Programming/Agent Model

NAF improves the logic programming/agent model, but it also highlights problems that need solutions for the model to show us the thinking that characterizes a rational agent.

1. ⊕ "[T]he human designer, after studying the world, uses the language of a particular logical system to give to our agent an initial set of beliefs `Delta_0` about what this world is like. In doing so, the designer works with a formal model of this world, W, and ensures that W ⊨ `Delta_0`. Following tradition, we refer to `Delta_0` as the agent’s (starting) knowledge base. (This terminology, given that we are talking about the agent’s beliefs, is known to be peculiar, but it persists.) Next, the agent ADJUSTS its knowledge base to produce a new one, `Delta_1`. We say that adjustment is carried out by way of an operation `ccA`; so A[`Delta_0`]= `Delta_1`. How does the adjustment process, `ccA`, work? ... [The adjustment] can come by way of any mode of reasoning.... The cycle continues when the agent ACTS on the environment, in an attempt to secure its goals. Acting, of course, can cause changes to the environment. At this point, the agent SENSES the environment, and this new information `Gamma_1` factors into the process of adjustment, so that `ccA[Delta_1 ∪ Gamma_1] = Delta_2`. The cycle of SENSES ⇒ ADJUSTS ⇒ ACTS continues to produce the life `Delta_0`, `Delta_1`, `Delta_2`,`Delta_3`…, … of our agent" (Stanford Encyclopedia of Philosophy, Artificial Intelligence). Suppose an agent notices that "not-φ" is a consequence of what he believes. Rationality permits him to add this consequence to his beliefs, but logic programming with NAF does not allow for this. Clauses have the form positive condition if positive conditions and not-conditions.

2. If an agent notices that a proposition φ is a defeasible consequence of what he believes, rationality permits him to add φ to his beliefs. Suppose that he notices and adds it. Suppose that subsequently he comes to believe some new proposition and sees that it defeats φ. Rationality permits him to retract his belief that φ, but there is no mechanism for this in our model as we are currently understanding it. At this point, we only know how to add beliefs.

3. Suppose an agent notices that a proposition is a consequence of what he believes. Rationality permits him to add the consequence to his beliefs, but he is not required to add it. He might instead decide to give up one of his existing beliefs, but we, again, do not know how to do this.

These three problems show that in the logic programming/agent model as it exists now, we need a better mechanism for updating beliefs in the KB. All we really have at this point in our model is the ability to determine logical consequence and the ability to determine NAF consequence. This is some intelligence, but rational agents have more intelligence than this.

Negation-As-Failure in Prolog

Here is an example Prolog program (based on the movie Pulp Fiction) with NAF (negation-as-failure). Suppose that Vincent enjoys every kind of burger except a Big Kahuna Burger.

enjoys(vincent,X) :- burger(X), \+ big_kahuna_burger(X).
burger(X) :- big_mac(X).
burger(X) :- big_kahuna_burger(X).
burger(X) :- whopper(X).
big_mac(a).
big_mac(c).
big_kahuna_burger(b).
whopper(d).

Suppose we ask whether there is something Vincent enjoys:

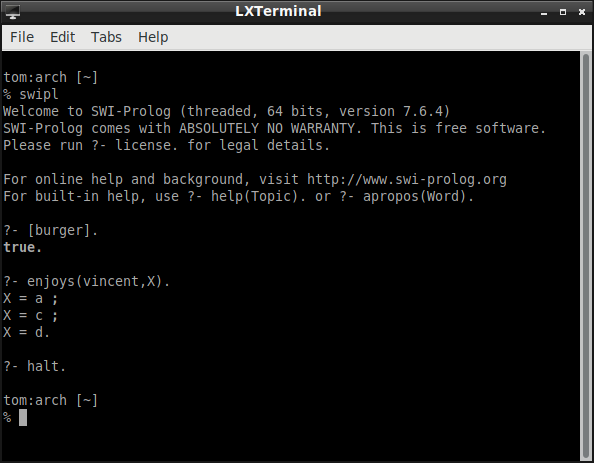
Given unification, the initial query

enjoys(vincent,X)

matches the head of the instance of the first rule

enjoys(vincent,a) :- burger(a), \+ big_kahuna_burger(a)

So the derived query is

burger(a), \+ big_kahuna_burger(a)

The first conjunct in this derived query matches the head of the instance of the second rule

burger(a) :- big_mac(a).

So the derived query becomes

big_mac(a), \+ big_kahuna_burger(a)

The first conjunct in this query matches the fact

big_mac(a)

So the derived query becomes

\+ big_kahuna_burger(a)

This "not" as NAF (\+) query succeeds if

big_kahuna_burger(a)

fails. It does fail. So

\+ big_kahuna_burger(a)

succeeds and hence

enjoys(vincent,a)

succeeds. One kind of burger Vincent enjoys is a Big Mac.

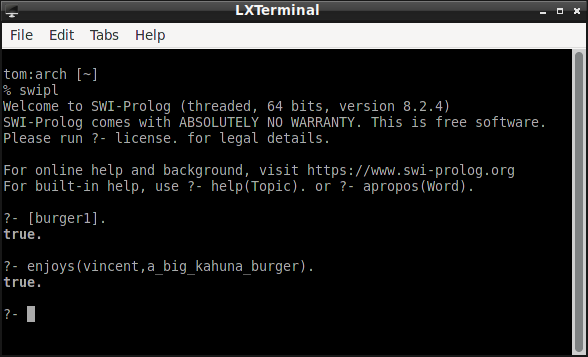
Another Example with NAF

Here is a variation on the "burger" example that is a little more like the "innocent unless proven guilty" example. The query asks whether Vincent enjoys a Big Kahuna burger. Given the first rule in his KB, he enjoys all burgers except those to which he is allergic. Since there is no proof he is allergic to Big Kahuna burgers, the query succeeds.

:- dynamic allergic/2.

enjoys(vincent,X) :- burger(X), \+ allergic(vincent,X).

%allergic(vincent,X) :- big_kahuna_burger(X).

burger(X) :- big_mac(X).
burger(X) :- big_kahuna_burger(X).
burger(X) :- whopper(X).

big_kahuna_burger(a_big_kahuna_burger).
big_mac(a_big_mac_burger).
whopper(a_whopper).

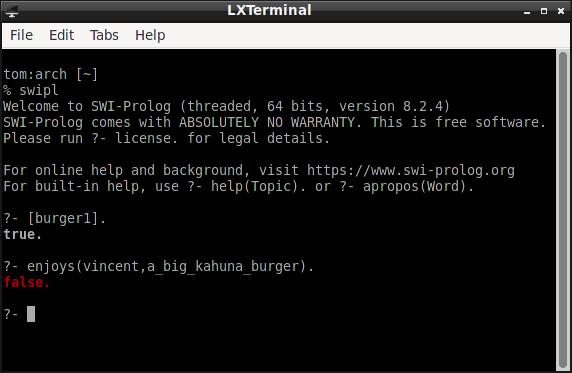
Here is what happens when the KB contains the new belief that Vincent is allergic to Big Kahuna Burgers. (To add the belief, uncomment the rule for predicate allergic.)

What we have Accomplished in this Lecture

We distinguished the Negation-as-Failure rule (NAF) from the Negation-Introduction (¬I) rule of logic. We identified NAF as a form of defeasible reasoning. We considered how to incorporate NAF into logic programming. We looked at Kowalski's use of NAF in his solution to the Byrne Suppression Task, and we raised some questions about whether his solution is adequate. We considered some of the problems that remain for using the logic programming with NAF/agent model. Finally, we saw NAF at work in some simple Prolog programs.