Philosophy, Computing, and Artificial Intelligence
PHI 319. The Computer Language Prolog.
 Thinking as Computation
Thinking as Computation
Chapter 3 (41-61), Chapter 4 (63-81), Appendix B-C (279-288)
Prolog programs (in a zip file)
Prolog ("PROgrammation en LOGique")
Prolog is a computer language based on logic programming. In this class (which is in philosophy, not computer science), we are not really interested in learning how to write Prolog programs. Our goal is to see that a machine can implement backward chaining. This demonstrates that we can create part of the intelligence of a rational agent.
There are two environments in which to run Prolog programs. You can download SWI Prolog to run them from the command line or use the online version to run them in a web browser.
The online version is easier for those without experience in computer programming.
An Introduction to Prolog Programs and Queries
Learn Prolog Now! is a helpful (and gentle) tutorial. Prolog programs are definite logic programs. As such, they include clauses (facts and rules) and queries. On the left, there are two clauses written as their interpretations in the propositional calculus. On the right, there are the corresponding ways they are written in Prolog notation.
a | a. (fact)
|
a ∨ ¬b ∨ ¬c | a :- b, c. (rule) (head :- tail.)
The following set of equivalences (which we considered in the last lecture) helps clarify the correspondence between the Prolog rule and its formulation in the propositional calculus:
a ∨ ¬b ∨ ¬c iff a ∨ ¬(b ∧ c)
(b ∧ c) → a
a ← (b ∧ c)
a :- b, c.
Queries represent negative clauses. (In the last lecture, we saw that a negative clause contains zero or more negative literals and no positive literals.) To get a better understanding of the relation between queries and clauses, consider the following negative clause:
¬a ∨ ¬b ∨ ¬c
This negative clause is truth-functionally equivalent to
¬(a ∧ b ∧ c)
The prompt in the Prolog interpreter is
?-
So an initial query looks a little like a formula equivalent to a negative clause
?- a, b, c.
The basic evaluation step of Prolog is the backward chaining computation we considered in the previous lectures. Here is a query, program clause, and derived query:
In Prolog In logic query ?-a,d,e. ¬a ∨ ¬d ∨ ¬e program clause a:-b,c. a ∨ ¬b ∨ ¬c derived query b,c,d,e. ¬b ∨ ¬c ∨ ¬d ∨ ¬e
The seminal paper is
J. A. Robinson's "A Machine-Oriented Logic Based on the Resolution Principle."
Journal of the Association for Computing Machinery, vol. 12, 1965, 23-41.
The resolution rule in
propositional logic is a derived deduction rule that produces
a new clause from two clauses with complementary
literals.
Literals are complimentary iff they are negations
of the other.
Here is a simple example of resolution:
a ∨ b ¬a ∨ c
-------------
b ∨ c
The derived query corresponds to the conclusion of an application of the derived deduction
rule called resolution. (A derived deduction rule is a deduction rule
for which there is a proof in terms of
the basic deduction rules. Derived deduction rules allow for shorter proofs.)
The resolution rule can be understood as a function that eliminates a pair of complementary literals and constructs a new
clause (the resolvent) from the literals that remain.
In terms of the matching procedure from the last lecture, the query (?-a,d,e.) is processed last-in, first-out. We search top-down for a clause whose head matches a. The match is with a:-b,c.. Its tail (b,c) is pushed onto the query list to form the derived query (b,c,d,e.).
The relation of logical consequence that the evaluation step represents is
{negative clause, program clause} ⊢ negative clause
A Screen Shot of Prolog in Action
This is not a course in computer programming, but you should play around some with Prolog.
Here (click the screenshot to enlarge it) is how the KB and the query look in the
online
version of Prolog:
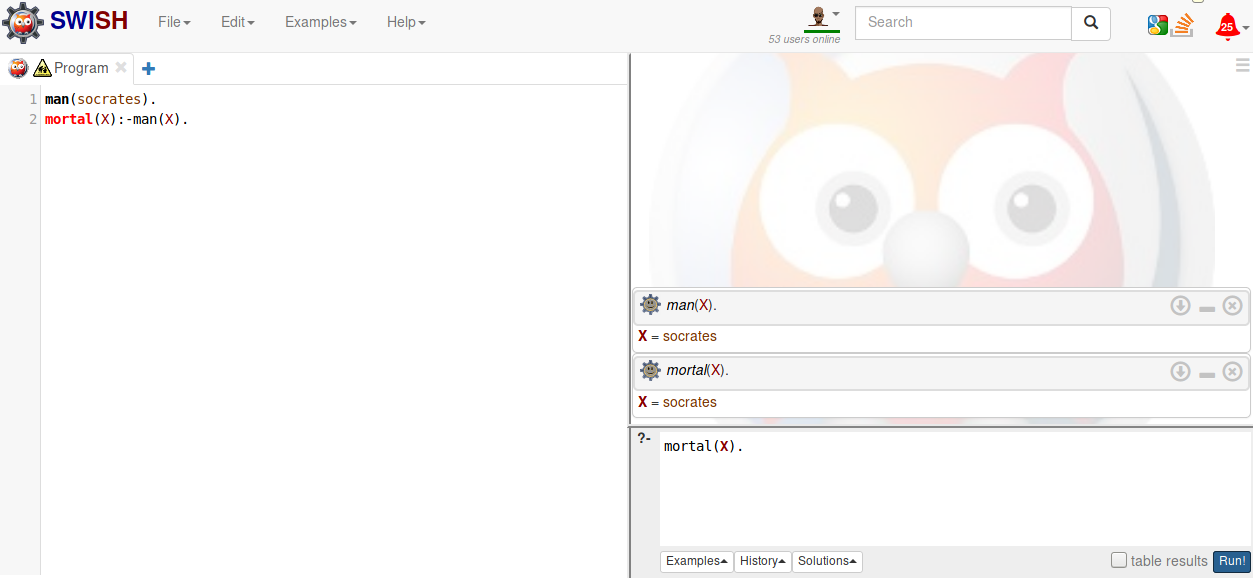 Below is a screen shot of my terminal.
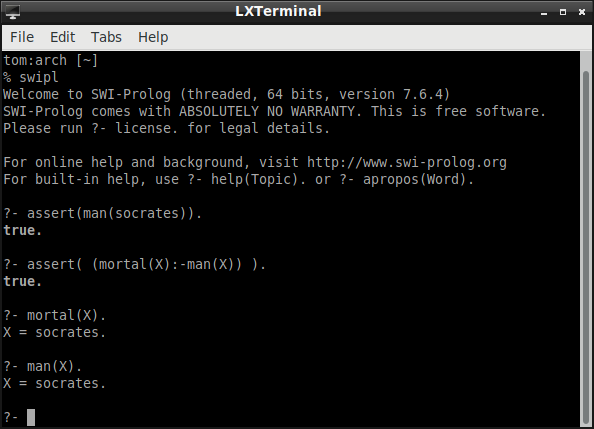
Below is a screen shot of my terminal.
I issue the command "swipl" to start the Prolog interpreter. In response, the interpreter issues the prompt (?-). This prompt signals that the interpreter is ready for a query. When we input a query, this can be understood as giving the interpreter a goal. I give it the goal of adding a fact (that "Socrates is a man" ) and a rule (that "Everything that is a man is mortal") to its KB. The interpreter returns "true" to indicate that it is has satisfied the goal. Now the KB is
man(socrates).
mortal(X):-man(X).
Next I pose two queries (is "something is mortal" and is "something is a man"). The queries give the interpreter the goal of determining whether the queries are logical consequences of the KB. Given the beliefs in the KB (that "socrates is man" and that "men are mortal"), Prolog should tell me that socrates is mortal and that he is a man. This in fact is what happens.
Prolog treats any term that begins with an uppercase letter (or the
underscore) as a variable. So in the rule
mortal(X):-man(X),
Prolog treats X as a variable.
Because the variable was in the supplied goals (mortal(X) and
man(X)) Prolog identifies the constant to which the variable is bound in
the computation (X = socrates).
For explanation of the database manipulation commands in Prolog, see
Database Manipulation in the tutorial.
The "Family" Example (Thinking as Computation, 42)
I consult the file family.pl. This file contains the program:
child(john,sue). child(john,sam).
child(jane,sue). child(jane,sam).
child(sue,george). child(sue,gina).
male(john). male(sam). male(george).
female(sue). female(jane). female(june).
parent(Y,X) :- child(X,Y).
father(Y,X) :- child(X,Y), male(Y).
opp_sex(X,Y) :- male(X), female(Y).
opp_sex(Y,X) :- male(X), female(Y).
grand_father(X,Z) :- father(X,Y), parent(Y,Z)
I pose a few queries.
I ask whether sue is the father of someone. The answer is "false."
I ask whether sam is the father of some female. The answer is "jane."
I ask whether sam is the child of someone. Prolog can disregard the current binding and look for another. This is what happens when I type ";" (which is logically equivalent to "or"). The first reply is john. I use the symbol ; to ask whether sam is the child of someone else. The answer is "john."
I ask whether president_crow is male.
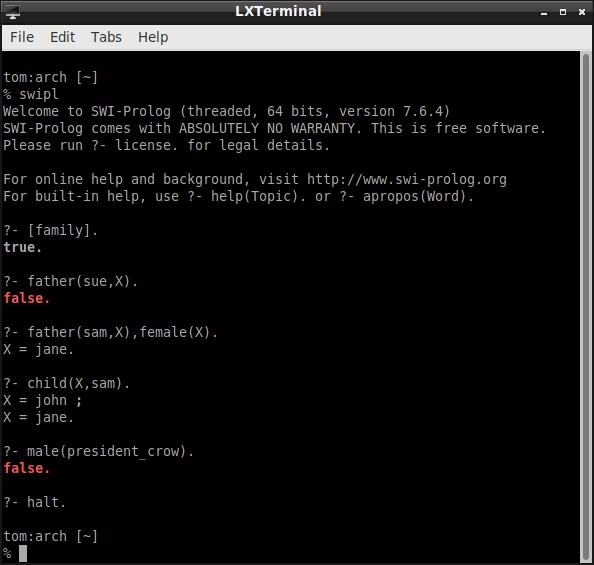
To test your understanding, consider the last query and reply in the family example. President Crow (of ASU) is male, but the Prolog interpreter responds with "false."
What is going on here?
To answer, explain what "false" means in the reply. It does not mean that the proposition expressed by "President Crow is male" is false. It means that something else is false. What is it?
A negative response means the query is not a logical consequence of the KB.
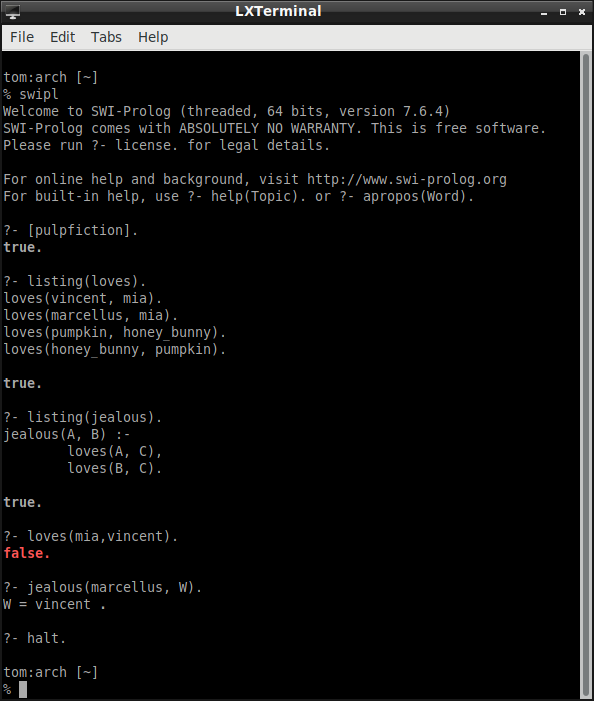
The Pulp Fiction Example
I consult the file (I created called) pulpfiction.pl. This file contains the program. I list the two predicates in the program. I pose a few queries. I halt the Prolog interpreter.
The "Blocks" Program
Here is the blocks program (blocks.pl) from the previous lecture:
on(b1,b2).
on(b3,b4).
on(b4,b5).
on(b5,b6).
above(X,Y) :- on(X,Y).
above(X,Y) :- on(X,Z), above(Z,Y).
This program consists in four facts (about which block is on top of which block) and two rules (that define the "above" relation). Corresponding to the facts and rules is the following model of the world (which, if you use your imagination, you can see as blocks on top of one another):
b3
b4
b1 b5
b2 b6
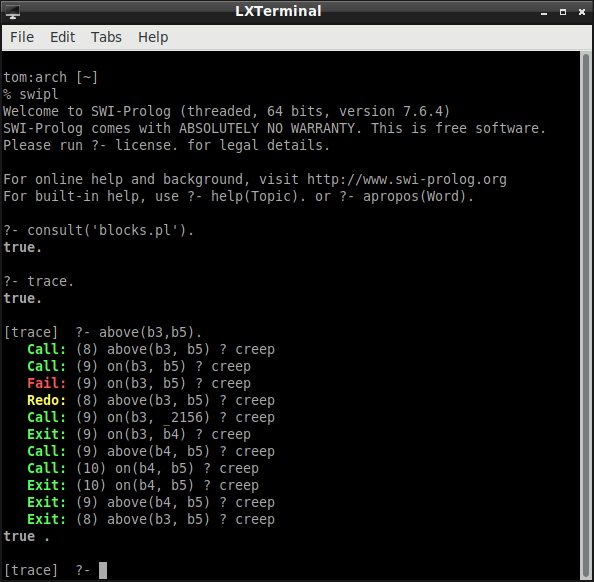
Here is the trace for "above(b3, b5)."
A trace provides information about the steps in the computation. In this course, it is not necessary to understand what the trace is saying. It is not hard to follow, though, given that you understand how the backward chaining computation works.
creep causes the debugger to single-step.
leap causes it to
resume running the program.
The query "above(b3, b5)" unifies with the first rule. The derived query is
"on(b3, b5)." This derived query fails. Now we have to try the query with the
second rule.
The second rule now takes the form
above(b3, b5) :- on(b3, _2156), above(_2156, b5).
"_2156" is a variable. Prolog renames variables in rules to prevent clashing.
The following helps show why we need to rename variables.
We can derive a contradiction from
∀xFa,x and ∀x¬Fx,b.
Why?
Fa,b follows from ∀xFa,x.
¬Fa,b follows from ∀x¬Fx,b.
As clauses, ∀xFa,x and ∀x¬Fx,b are Fa,x and ¬Fx,b.
Suppose that the KB is
Fa,x.
and the query is
?-Fx,b.
The query asks whether there is an x in the F relation to b.
There is. Fa,b is a logical consequence of ∀xFa,x.
Suppose that instead of renaming, we try to unify by substituting a for x
in the query and the fact in the KB.
The result is Fa,b and Fa,a, and they do not match.
Further, because the variable clashes, we cannot make them match.
The derived query list is "on(b3, b4), above(b4, b5)." These queries succeed.
The derived query list is now empty, and this means that the original query succeeds.
Some Explanation of Lists in Prolog
We will uses lists in Prolog later in the course when we come to natural
language processing (NLP).
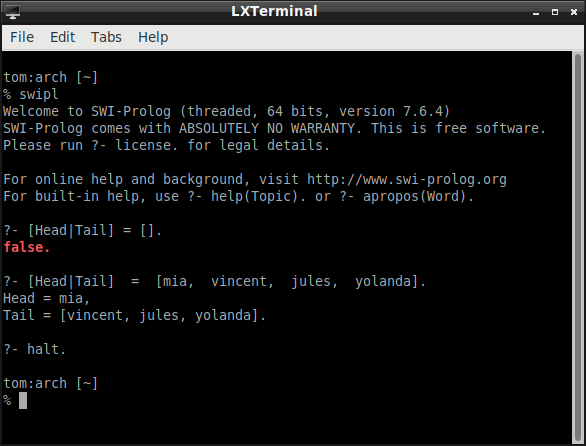
Lists are a finite sequence of elements. They are specified in Prolog
by separating the elements by commas and enclosing them in square brackets.
The empty list is a list.
A non-empty list has a head and a tail. The head is the first element. The tail is the rest. Prolog has a built-in operator | to decompose a list into its head and tail.
We will use lists when consider the intelligence in understanding natural language.
What we have Accomplished in this Lecture
We have become familiar with some of the basics of programming in Prolog. In doing so, we have seen how Prolog incorporates some of the principles of logic programming.
This shows that a machine can implement one form of intelligence. Given a set of premises and a query, it can answer positively if the query is a logical consequence of the premises.
This obviously does not solve "the problem of AI," but it is a step forward.

