Philosophy, Computing, and Artificial Intelligence
PHI 319. The Observation-Thought-Decision-Action Cycle.
We saw an attempt to implement the observation-thought-decision-action cycle on a machine. To make more progress, we need to think more carefully about the steps in the cycle.
The Cycle as a Sequence of Instructions
The cycle, in the "Fox and Crow" example, begins when the fox realizes it is hungry. The fox, as a machine, has sensors. The information the sensors provide become beliefs in the KB.
We can think of this step in the cycle as revising the beliefs in the KB based on the information perception provides. For the fox, we add the proposition that he is hungry to his KB.
The process of revising beliefs based on the arrival of new information consists in more than adding new beliefs. Sometimes beliefs must also be removed from the the KB, but rather than worry about the details, We are going to pretend that we have a function, revise, that returns a revised set of beliefs given a set of beliefs and an observation (a percept).
At this point, then, the observation-thought-decision-action cycle looks something like this:
1. KB ← KBo; /* KBo are the initial beliefs */
2. while alive do
3. get next percept p;
4. KB ← revise (KB, p);
?.
?. end-while
The fox has a set of initial beliefs. The fox makes an observation ("get next percept p"), and the fox revises his KB on the basis of this observation. Some other things happen. The cycle repeats.
What are the "others things [that] happen"?
In the case of the fox, the observation led to a belief ("I am hungry") that triggered a maintenance goal. The maintenance goal, in turn, gave rise to an achievement goal.
Achievement goals function like desires. The fox gets the desire to have food and eat it.
To get such desires, we can pretend we have a function, options, that returns a set of desires (achievement goals) given the KB and the set of maintenance goals the agent possesses.
1. KB ← KBo; /* KBo are the initial beliefs */
2. while alive do
3. get next percept p;
4. KB ← revise (KB, p);
5. D ← options (KB, MG);
?.
?. end-while
Intentions and Plans in Practical Reasoning
Once we have the set of desires (achievement goals),
we need a way to select the one the agent intends to pursue now. This what the agent currently intends to do,
and we can pretend we have
Michael Bratman (in Intentions, Plans, and Practical Reason
(Harvard University Press, 1987)) argues that
rational agents tend to
commit themselves to their intentions and thus tend not to interrupt this
commitment by recalculating their desires and forming new intentions.
To understand Bratman's idea, notice that steps (3) - (6) in the algorithm do not occur instantaneously. They take
time, and the world might have changed during this time in such a way that
the agent would have formed a new set of intentions if he were to recalculate.
There are limits to the extent of an agent's commitment to an intention before it is acting irrationally,
but the agent must sometimes commit itself if it is ever to
do anything more than calculate its intentions.
a function, filter, that returns this intention given the KB and the set
of desires.
1. KB ← KBo; /* KBo are the initial beliefs */
2. while alive do
3. get next percept p;
4. KB ← revise (KB, p);
5. D ← options (KB, MG);
6. I ← filter (KB, D);
?.
?. end-while
Given the intention, what is the mechanism for achieving it?
The agent, it seems, must have plans.
The agent can construct them or retrieve them from a plan library. To get the plan, we can pretend we have a function, plan, that returns a plan given the KB and the intention.
1. KB ← KBo; /* KBo are the initial beliefs */
2. while alive do
3. get next percept p;
4. KB ← revise (KB, p);
5. D ← options (KB, MG);
6. I ← filter (KB, D);
7. π ← plan (KB, I);
8. execute (π)
9. end-while
What happens in the function "execute (π)"?
One possibility is that the agent executes the steps in the plan until it is empty:
1. KB ← KBo; /* KBo are the initial beliefs */
2. while alive do
3. get next percept p;
4. KB ← revise (KB, p);
5. D ← options (KB, MG);
6. I ← filter (KB, D);
7. π ← plan (KB, I);
8. while not empty (π) do
9. α ← head of π;
10. execute (α);
11. π ← tail of π;
12. end-while
13. end-while
This gives the agent some but not much intelligence.
The fox, for example, would not be very intelligent if it were to praise the crow and then were to try to pick up the cheese whether or not the crow drops it.
The agent, then, does not have much intelligence if executes its plan one step at a time without thinking about how the world might have changed in the time it takes to execute the plan.
Logic-Based Production Systems
Kowalski's Logic-Based Production System (LPS) For brief explanations of LPS, see How to do it with LPS (Logic-based Production System) and LPS. is an extension of logic programming (LP). The idea is to supplement LP with the observation-thought-decision-action cycle.
The resulting model of intelligence is interesting, but it takes some effort to see it.
The following is a
program
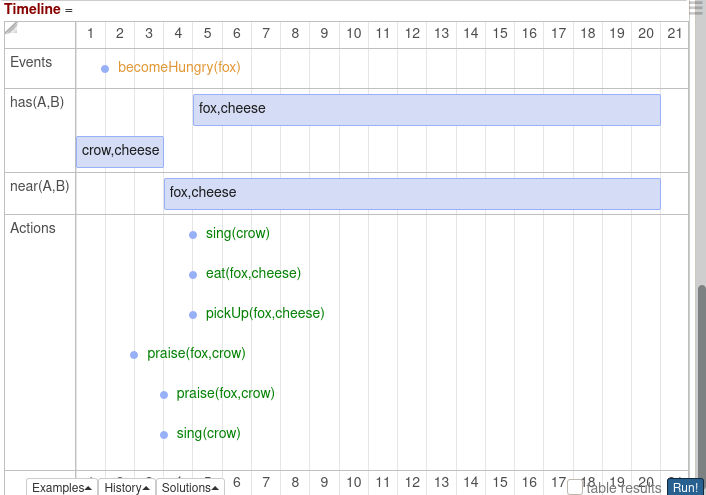
for a version of the fox and the crow example. The graph (in the side notes) shows how the timeline unfolds
when the program is run.
fluents has/2, near/2.
events becomeHungry/1, beNear/2.
actions sing/1, obtain/2, eat/2, praise/2, pickUp/2.
food(cheese).
initially has(crow, cheese).
observe becomeHungry(fox) from 1.
if becomeHungry(Agent)
then food(X), obtain(Agent, X), eat(Agent, X).
if praise(Agent, crow)
then sing(crow).
obtain(Agent, Object)
if beNear(Agent, Object),
near(Agent, Object),
pickUp(Agent, Object).
beNear(fox, cheese)
if has(crow, cheese),
praise(fox, crow).
sing(crow) terminates has(crow, cheese)
if has(crow, cheese).
sing(crow) initiates near(fox, cheese)
if has(crow, cheese).
pickUp(Agent, Object) initiates has(Agent, Object).
1. KB ← KBo; /* KBo are the initial beliefs */
2. while alive do
3. get next percept p;
4. KB ← revise (KB, p);
?.
?. end-while
We can see in the graph of this program that the fox, at time 1, observes it has become hungry and thus
forms the belief in its KB that it is hungry.
Once the fox has this belief, because of how its mind works, it gets the achievement goal
to obtain and eat some food:
food(X), obtain(fox, X), eat(fox, X)
To achieve the first goal on this list of achievement goals, the fox first passes "food(X)" as a query to its KB. The reply is that "cheese" is a food. This in turn transforms the list of achievement goals so that it is
obtain(fox, cheese), eat(fox, cheese)
The fox's achievement goal initially is
to make it true that there is a food, that the fox obtain it, and that the fox eat it. The only way
to make this true is to make an instance of it be true.
1. KB ← KBo; /* KBo are the initial beliefs */
2. while alive do
3. get next percept p;
4. KB ← revise (KB, p);
5. D ← options (KB, MG);
6. I ← filter (KB, D);
?.
?. end-while
In passing "food(X)" as a query to its KB, the fox is asking itself whether "∃X food(X)" is a logical consequence of what it believes in order
to give itself an instance of the indefinite goal it can try to achieve. The fox thinks that cheese is
food and what it is trying to obtain and eat.
The next step in the fox's thinking requires some reflection to work out.
The fox passes "obtain(fox cheese)" to its KB. In fox's KB, there is a rule for "obtain(fox, cheese)." This rule, though, is not quite what we would expect from the point of view of logic programming. The rule contains "events," "actions," and "fluents."
What are these things?
Events and actions change state. A fluent is a state that can change over time.
The rule, then, in the fox's KB for "obtain(Agent, Object)" says in part that
"obtain(Agent, Object)" is true if the event "beNear(Agent, Object)" happens.
"beNear" and "pickUp" are in lower camel case. This practice writes
without spaces or punctuation. The first word is in lower case. Subsequent words
begin in upper case.
1. KB ← KBo; /* KBo are the initial beliefs */
2. while alive do
3. get next percept p;
4. KB ← revise (KB, p);
5. D ← options (KB, MG);
6. I ← filter (KB, D);
7. π ← plan (KB, I);
8. while not empty (π) do
9. α ← head of π;
10. execute (α);
11. π ← tail of π;
12. end-while
13. end-while
This event can only happen if an instance of it happens. The fox has a rule for one instance. The
instance of "beNear(Agent, Object)" is the event "beNear(fox, cheese)."
The rule for "beNear(fox, cheese)" says that this event happens if "has(crow, cheese)"
is true and the fox makes "praise(fox, crow)" true. The fox can make "praise(fox, crow)" true because "praise" is a basic
action for the fox.
So by passing "obtain(fox cheese)" to its KB, the fox is really doing two things. It is checking whether this part of its achievement goal is a logical consequence of its KB, and it is taking action to make it a logical consequence if it determines that it is not a logical consequence.
What we have Accomplished in this Lecture
We saw in the last lecture on the "fox and crow" that it is not straightforward to incorporate the thinking involved in achieving an achievement goal into the logic programming/agent model. In this lecture, to move forward, we tried to set out the steps in the observation-thought-decision-action cycle as sequence of instructions in an algorithm. Further, we briefly considered Kowalski's Logic-Based Production System (LPS) programs. These programs attempt to combine logic programming with an observation-thought-decision-action cycle.

