Philosophy, Computing, and Artificial Intelligence

Computational Logic and Human Thinking
Chapter 16 (217-231)

How to Explain the Results in the Wason Selection

Kowalski argues that the hypothesis that humans do not naturally develop a capacity for logical deduction is not the only way to account for the results of the Wason Selection Task.

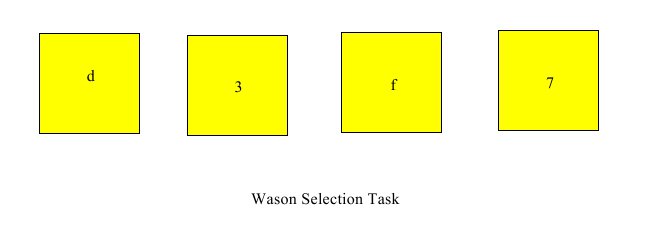⊕ In the Wason Selection Task, the experimenters give the subjects a "task" to perform. The task is to make a certain selection among presented options. The experimenters pose this task in terms of cards the subject can see. There are four cards with letters on one side and numbers on the other. One side of each card is showing.

The subject in the Wason Selection Task is asked to select those and only those cards that must be turned over to determine whether the following statement is true:

(*) if a card X has letter d on the letter side, then the card X has number 3 on the number side

The Expected Results

The experimenters expect the subjects to check two cards:

modus ponens:
from observation φ ("d"), check for ψ ("3") on the number side.
modus tollens:
from observation ¬ψ ("7), check for ¬φ ("not d") on the letter side

The Observed Results

Most subjects perform modus ponens but fail to perform modus tollens. In addition, many subjects perform the fallacy (from a classical logic point of view) of affirming the consequent:

affirm the consequent:
from observation ψ ("3"), check for φ ("d") on the letter side

Kowalski's Explanation of the Observed Results

Kowalski stresses that to understand the observed results, it is necessary to appreciate that the subjects interpret the words they hear in ways the experimenters do not expect.

He summarizes this idea in the equation "natural language understanding = translation into logical form + general purpose reasoning" (Computational Logic and Human Thinking, 217).

The experimenters assume that (*) has the logical form of a material conditional (φ → ψ), but Kowalski suggests that not all of the subjects understand the sentence in this way.

How, then, do they understand the sentence (or "translate it into logical form")?

"In our agent model, the agent’s response depends upon whether the agent interprets the conditional as a goal or as a belief" (Computational Logic and Human Thinking, 218).

The conditional as a belief: why subjects perform modus ponens

⊕ "Modus Ponens. In Computational Logic, conditional beliefs are used to reason both backwards and forwards. In particular, given a (passive) observation of a positive predicate P, forward reasoning with the conditional if P then Q derives the positive conclusion Q. This is a classically correct application of modus ponens..." (Robert Kowalski, Computational Logic and Human Thinking, 221).

"Affirmation of the Consequent. In Computational Logic, conditionals are also used to explain observations. Given an observation of Q, backward reasoning derives P as a candidate explanation of Q. This derivation can be viewed ... as abduction with the conditional if P then Q ..." (Robert Kowalski, Computational Logic and Human Thinking, 221).


Given Kowalski's explanation of why the agents perform modus ponens and affirm the consequent, it seems that subjects should perform them in equal numbers. This, however, is not what happens in the experiment. On the logic programming/agent model, agents can use their beliefs to reason forward from observations.

This, Kowalski seems to claim, explains why subjects perform modus ponens (select the first card). If they incorporate the conditional as a belief, it is natural to fall into forward reasoning when they observe "d."

The conditional as a belief: why subjects affirm the consequent

⊕ On the logic programming/agent model, agents use their beliefs in forward reasoning but also in abductive reasoning. In abductive reasoning, they use their beliefs to explain their observations.

This, Kowalski seems to claim, explains why subjects affirm the consequent (select the second card). If they incorporate the conditional as a belief, it is natural to fall into abductive reasoning when they observe "3."

The conditional as a belief: why subjects fail to perform modus tollens

When the subjects look at the fourth card, they observe "7." To perform modus tollens with

(*) if a card X has letter d on the letter side, then the card X has number 3 on the number side

they must first know that the negative statement

it is not the case that the fourth card has number 3 on the number side

is a consequence of their observation ("7"). This, however, according to Kowalski, is not easy for the subject to know because the observation ("7") does not identify the the query

the fourth card has number 3 on the number side

the subject must use in reasoning to know the negative statement is a consequence of the observation ("7").

Kowalski says that this explains why so many subjects fail to perform modus tollens.

The conditional as a goal: why subjects perform modus tollens

Knowalski argues that subjects do better with "meaningful" conditionals, such as

If a person is drinking in a bar, then the person is at least twenty-one years of old

⊕ "In this book, we have seen a variety of uses for an agent's conditional goals. Their primary use is [as a maintenance goal] to help the agent maintain a harmonious personal relationship with the changing state of the world. However, conditional goals can also serve a secondary function of helping to maintain harmony in a society of agents as a whole. In both cases, conditional goals regulate the behaviour of agents, both generating and preventing actions that change the state of the world" (Robert Kowalski, Computational Logic and Human Thinking, 225). because it is natural for them to treat the truth of this sentence as a conditional goal he is tasked to enforce (similar to an integrity constraint on the world or on society).

This, Kowalski claims, explains why subjects perform modus tollens with these "meaningful" conditionals.

If the agent observes an underage person, the agent will need to make sure the antecedent fails. So he will observe whether the person is drinking in a bar. If the person is, the rule is violated. In this way, the subjects interpret

If a person is drinking in a bar, then the person is at least twenty-one years of old

as an integrity constraint on society

If X is drinking alcohol in a bar and X is under twenty-one years of old, then false

Once the agent observes an underage person, the agent will need to make sure that the person is not drinking in a bar. Otherwise there is violation of "integrity" the agent is tasked to enforce.

The conditional as a goal: why subjects fail to perform affirm the consequent

This also helps explains why the subjects do not affirm the consequent. The observation of the truth of the consequent of the rule the agent is trying to enforce does not trigger reasoning.

What we have accomplished in this lecture

We considered Kowalski's explanation of the results of the Wason Selection Task and why subjects tend to reason better with more meaningful conditionals. He argues that "the agent’s response depends upon whether the agent interprets the conditional as a goal or as a belief" (Computational Logic and Human Thinking, 218). This is an interesting explanation, but one might wonder why the subjects "interpret the conditional" in these ways. These two "interpretations" do not appear essential the logic programming/agent model.